هذا المقال مقتبس من كتاب لجيمس ستونز صدر حديثاً بعنوان " نظرية المعلومات: مقدمة تعليمية"
نحن جميعاً مطّلعون على القياسات والوحدات، فنعلم أن الدقيقة هي جزء من الزمن، والمتر جزء من الطول، والبت هو جزء من المعلومات. دعنا نتحدث حول البت، ماذا نعني بجزء من المعلومات؟ لماذا البت (bits) يُعبّر عن أجزاء المعلومات بطريقة صحيحة؟ وكيف ترتبط هذه الوحدة بالأرقام الثنائية (النظام الثنائي)، أي بـ 0 و1؟
العثور على طريق، بت بعد بت:
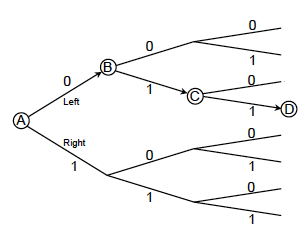
(البت) هو مقدار كمية المعلومات التي تحتاجها للاختيار بين بديلين محتملين متساويين. تخيل أنك تقف على مفترق طرق في النقطة (A) في الشكل الموجود في الأسفل، وأنت ترغب في الوصول إلى النقطة (D).
لاحظ أن هذا الشكل يمثل النظر بعين طائر، وهذا ما لا تستطيع أن تفعله بعينيك على أرض الواقع، فكل ما تملكه هو مفترق أمامك، وقرار عليك اتخاذه. إذا كنت لا تمتلك معلومات مسبقة حول أي طريق ستختار، سيكون لديك احتمالان (أي طريقان من المحتمل سلوكهما) وهذان الاحتمالان متساويان. فإذا أخبرتك بالذهاب شمالاً، ستكون قد استقبلت واحد بت من المعلومات؛ أي إذا قمنا بتمثيل إرشاداتي بالنظام الثنائي (0 = يسار و1 = يمين)، سيكون هذا الرقم الثنائي قد زودك بواحد بت من المعلومات تخبرك أي طريقٍ عليك أن تسلك. في الواقع، يُمكن استخدام الأرقام الثنائية (0-1)، في تمثيل الرحلة كاملة من A وصولاً إلى D.
تخيل أنك كنت في نزهة على الطريق وجئت إلى مفترق آخر عند النقطة (B) في الشكل. مرة أخرى، ولعدم امتلاكك أدنى فكرة أي طريق ستختار، فإن العدد الثنائي (1= يمين) يعطيك بت واحد من المعلومات، ويسمح لك باختيار الطريق الصحيح الذي يقودك إلى النقطة (C).
لاحظ أنّ C هي واحدة من أربع وجهات مرحلية من الممكن أن تصلها بعد اتخاذ قرارين اثنين. ويسمح لك الرقمان الثنائيان باتخاذ قرارات صحيحة تعطيك اثنين بت من المعلومات، مما يتيح لك الاختيار بين أربعة بدائل ممكنة (باحتمالات متساوية)، والرقم 4 أربعة ينتج عن \(2×2=2^2\)
يُوفر لك الرقم الثنائي الثالث (1 = يمين) بت إضافي من المعلومات، مما يسمح لك مرة أخرى باختيار الطريق الصحيح، فيقودك إلى النقطة D.
الآن، هناك ثمانية طرق يمكن اختيارها منذ البداية عندما بدأت في A، لذلك الأرقام الثلاثة الثنائية، التي وفرت ثلاثة بت من المعلومات، سمحت لك بالاختيار بين ثماني بدائل متساوية الاحتمال؛ حيث أن الرقم 8 ينتج عن \(2×2×2=2^3\)
لاحظ أنّ القرار الذي تم اتخاذه في A، استبعد نصف الوجهات الثمانية الممكنة والمبينة في الشكل الذي عملت عليه. وبالمثل، فإن القرار الذي تم اتخاذه في كل مفترق على التوالي خفّض من عدد الوجهات المحتملة المتبقية إلى النصف في كل مرة.
رحلة من ثمان بدائل:
يمكننا أن نكرر هذا بشكل أعم، فإذا استخدمنا (n) لتمثيل عدد المفترقات، و(m) لتمثيل عدد الوجهات النهائية، إذا قابلت n من المفترقات فإنك تكون قد اخترت بشكل فعال:
\(m=2^n\)
من الوجهات النهائية.
لأن القرار عند كل مفترق يتطلب بت واحد من المعلومات، فـ n من المفترقات يتطلب عدد n بت من المعلومات، ليسمح لك بالاختيار من 2ⁿ بديل متساوية الاحتمال.
نستطيع تسمية كل وجهة من الوجهات الثماني الممكنة بعدد عشري بين 0 و7، أو بما يعادله من رقم ثنائي كما في الشكل أدناه، هذه الأرقام العشرية ومعادِلاتها من الأرقام الثنائية موضحة في الجدول.
العد في النظام الثنائي مماثل للعد بالنظام العشري، شاهد الرابط هنا لمعرفة كيفية القيام بذلك.
للتمثيل الثنائي للأرقام العديد من المزايا، فعلى سبيل المثال، يُشير العدد الثنائي إلى وِجهة (على سبيل المثال 011)، يمثل هذا الرقم بشكل صريح مجموعة من تعليمات اليمين/اليسار المطلوبة للوصول إلى هذه الوجهة، ويُمكن استخدام هذا التمثيل في أي مشكلة تتطلب عدد من القرارات (أي ثنائية) ثنائية الاتجاه.
رحلة قرارات \(log_2(8)\):
يُمكن تمثيل تعقيد (complexity) أي رحلة إما بعدد الوجهات النهائية، أو بعدد المفترقات في الطريق الذي يجب اجتيازه للوصول إلى الوجهة المطلوبة.
نعلم أنه كلما ازداد عدد المفترقات، ازداد عدد الوجهات الممكنة. وكما رأينا الآن، إذا كان هناك ثلاث مفترقات، سيكون هناك \(8=2^3\) وجهات ممكنة.
من منظور آخر، إذا كان هناك ثمان (m= 8) وجهات ممكنة، إذن كم سيكون عدد المفترقات n؟ بعبارة أخرى، معطى ثماني وجهات، ما هو قيمة القوة المرفوعة على 2 المطلوبة لنحصل على عدد 8؟ في هذه الحالة، نحن نعلم أن الإجابة هي n=3، والتي تدعى لوغيرتم 8 إلى القاعدة 2.
لذلك \(3=log_2(8)\) هو عدد المفترقات التي ستؤدي إلى الوجهات الثمان.
بشكل أعم، لوغاريتم إلى القاعدة 2 لـ m هي الأس أو القوة التي يجب أن تضاف لإيجاد m. وبشكل مكافيء، الرقم m هو الرقم الذي نود التعبير عن بواسطة اللوغيرتم.
\(n=log_2m\)
الآن، ذلك ما نعرفه عن اللوغيرتمات، ونستطيع تلخيص رحلتك من مناظير مختلفة بدلالة البت "وحدة قياس المعلومات": إذا كان عليك أن تختار بين عدد m من البدائل متساوية الاحتمال، أنت تحتاج إلى عدد \(n=log_2 m\) من البت من المعلومات.
مليون إجابة لعشرين سؤال:
التنقل خلال سلسلة من المفترقات في طريق شبيهٌ -في بعض النواحي- بلعبة العشرين سؤالاً.
في هذه اللعبة يختار خصمك كلمة (عادة تكون اسم)، وأنت (كسائلٍ فطن) مسموح لك أن تسأل عشرين سؤالاً لاكتشاف ما هي هذه الكلمة، والأهم من ذلك، كل سؤال يجب أن تكون إجابته نعم/لا (أي نظام ثنائي)، وبالتالي فإن الجواب يعطيك على الأقل بت واحد من المعلومات.
لماذا على الأكثر؟
قياساً على مثال التنقل، حيث أدى كل قرار على مفترق طرق إلى تقليل عدد الوجهات المتبقية إلى النصف، يجب أن يُخفض كل سؤال عدد الكلمات المتبقية الممكنة إلى النصف، والسؤال الذي تعرف جوابه مسبقاً هو خيار سيء.
مثلاً، إذا كان سؤالك: "هل الكلمة في القاموس؟"، إذن الإجابة تكاد تكون مؤكدة "بنعم!"، وهو جواب متوقع ولا يعطيك أي معلومات.
وعلى العكس، السؤال الذكي الذي يتم اختياره بعناية، هو سؤال ليس لديك أي فكرة عما إذا كانت الإجابة عليه ستكون بنعم أو لا - هناك فرصة 50:50 للإجابة بنعم أو لا. في هذه الحالة، يُوفر الجواب بالضبط واحد بت من المعلومات، والنسخة المختصرة من العشرين سؤالاً في الشكل أدناه تشرح بشكل أكثر وضوحاً.
في هذه اللعبة، لدى خصمك ثماني مفردات بالضبط، وأنت تعرف ما هي هذه الكلمات. وسؤالك الأول (Q1) يمكن أن يكون، "هل هو جماد؟"
يجب أن تُخفض الإجابة من عدد الكلمات الممكنة إلى أربع (أي إلى النصف)، ويقودنا ذلك إلى سؤالك الثاني (Q2): "هل هو حيوان ثديي؟"، وأيضاً على الإجابة تقليل عدد الكلمات الممكنة إلى النصف، وذلك يقود إلى سؤالك الثالث.
بحلول الوقت الذي تصل فيه إلى السؤال الثالث (Q3) سيتبقى إجابتان اثنتان لا غير، وبعدما تسأل السؤال الثالث (هل هي قطة؟)، ردّ خصمك بنعم أو لا يقودك إلى الإجابة الصحيحة.
باختصار، أنت سألت ثلاثة أسئلة، واستبعدت جميع الكلمات الثماني الممكنة عدا كلمة واحدة -هي الإجابة الصحيحة.
بشكل أكثر واقعية، لنفترض أن خصمك لديه نفس المفردات كما لديك، فمعظمنا لديه مفردات متماثلة، ولذلك فهذا الافتراض منطقي إلى حد كبير.
على وجه التحديد، دعونا نفترض أن هذه المفردات تحتوي بالضبط على 1,048,576 كلمة. بمعرفتك بهذا مسبقاً، على كل سؤال تختاره أن يكون قادراً على تخفيض عدد الكلمات الممكنة المتبقية إلى النصف، ولذلك في عالم مثالي، سيُخفض سؤالك الأول عدد الكلمات الممكنة إلى 525,288، وسؤالك التالي سيخفضها العدد إلى 262,144 كلمة.. وهكذا. وبحلول الوقت وعندما تصل إلى السؤال التاسع عشر، يجب أن يكون قد بقي فقط سؤالين اثنين، وبعد السؤال العشرين، يجب أن تتبقى كلمة واحدة فقط.
السبب الكامن وراء عمل ذلك بدقة كبيرة هو أن الأسئلة العشرين تسمح لك بالاختيار بين \(1,048,576=2^{20}\) كلمات متساوية الاحتمال -أي حوالي المليون، لذلك منحتك الـ 20 بت من المعلومات، التي حصلت عليها من خلال طرحك للأسئلة، القدرة على تضييق نطاق الكلمات المحتملة من حوالي مليون كلمة إلى كلمة واحدة.
بعبارة أخرى، سمحت الأسئلة العشرون بالعثور على الكلمة الصحيحة من أصل حوالي مليون كلمة محتملة. وتشير التقديرات أن الشخص العادي لديه مفردات أقل من 20,000 كلمة، لذلك فإن عشرين سؤالاً يتم اختيارها بعناية تكفي بسهولة لتحقيق الفوز في هذه اللعبة.
إنّ إضافة سؤال آخر لن يؤدي فقط إلى خلق لعبة جديدة هي "21 سؤال"، بل ربما سيؤدي أيضا إلى مضاعفة عدد الكلمة الممكنة إلى حوالي 2 مليون، وكل ذلك يُمكن تضييقه إلى كلمة واحدة.
بكلماتٍ أخرى، يسمح كل سؤال إضافي لك بالحصول على بت واحد إضافي من المعلومات، وبالتالي يمكن أن يضاعف العدد الأولي من الكلمات. من حيث المبدأ، تسمح لك لعبة مكونة من أربعين سؤالاً بالحصول على 40 بت من المعلومات، وستسمح لك بدورها إيجاد كلمة واحدة من \(2^{40} \approx 10^{12}\) كلمة.
لنعود إلى مثال التنقل، سيسمح لك 40 بت بالتنقل في 40 مفترق في الطريق، ويُتيح لك أيضا اختيار واحد من حوالي تريليون طريقة ممكنة؛ ولذلك في المرة القادمة وعندما تصل وجهتك بعد رحلة تتضمن 40 قراراً، تذكر أنك تجنبت الوصول إلى تريليون إلا واحد وجهة خاطئة.
المعلومات، والبتات، والأعداد الثنائية:
على الرغم من أن كلمة "بت" مشتقة من "رقم ثنائي" وذلك بناء على بنية الكلمتين في اللغة الإنجليزية، إلا أنه هناك فرق دقيق ولكن حيوي بينهما، فالعدد الثنائي هو قيمة المتغير الثنائي، حيث أن القيمة ممكن أن تكون 0 أو 1، لكن الرقم الثنائي ليس المعلومة بحد ذاتها.
في المقابل، البت هو كمية معينة من المعلومات، البتات (جمع بت) والأعداد الثنائية ذوات كينونة مختلفة النوع، والخلط بينها يُعرف بخطأ التصنيف (category error).
لشرح هذه النقطة، انظر إلى المثالين اللذين يعبران عن جهتين في التفكير، ففي الجهة الأولى: إذا كنت تعرف أنه عليك أن تأخذ الطريق الأيسر من النقطة A، وأنا أعطيت لك العدد الثنائي (0 =اليسار)، سيكون لديك عدد ثنائي لكنك لم تحصل على معلومات حينئذ.
من جهة أخرى، إذا لم يكن لديك أدنى معلومة حول أي طريق عليك أن تختار، وأعطيت لك العدد الثنائي 0، يكون قد تم اعطاؤك عدد ثنائي وحصلت على بت واحد من المعلومات بين الجهتين.فإذا أخبرك أحدهم أن احتمالية أن يكون الطريق الأيسر هو الصحيح 71%، وأنا أكدت لك ذلك تباعاً بإعطائك الرقم الثنائي 0، حينها يُشير هذا الرقم (0) إلى أقل من بت من المعلومات لأنك تعرف بعض المعلومات حول الطريق الذي يجب أن تسلكه.
في الحقيقة، يمكن القول أنه عندما تستقبل مني رقم 0، يمكنك على وجه التحديد الحصول على نصف بت من المعلومات، ويمكن أن ترى الإثبات في الفصل الخامس من كتاب "نظرية المعلومات: مقدمة تعليمية"؛ وهكذا، على الرغم من أنني لا أستطيع أن أعطيك نصف عدد ثنائي، إلا أنه بإمكاني استخدام عدد ثنائي لأعطيك نصف بت من المعلومات.
من المحزن أنه في الاستعمال الحديث، أصبح كلٌ من وحدة البت والرقم الثنائي مترادفين، واقترح ديفيد ماكاي David MacKay أن وحدة المعلومات يجب أن تُستبدل بمصطلح يطلق عليه "شانون" تكريماً لكلاود شانون Claude Shannon الأب الروحي لنظرية المعلومات، ولمعرفة المزيد عن ذلك زر الرابط التالي
عن الكاتب:
"جيمس ستون" قارئ في علم الأعصاب الحاسوبية في جامعة شيفيلد-إنجلترا، وتم اقتباس هذا المقال من كتابه الذي نشره مؤخراً "نظرية المعلومات: مقدمة تعليمية".