أَعتبر المعادلة التالية واحدةً من أفضل النتائج الرياضية لديّ
(1)
\( \frac{ \pi} 4=1-\frac{1}3+\frac{1}5-\frac{1}7+\frac{1}9+....\)
كل ما يهمني هنا هو أن الرياضيات كلَّها تجتمعُ في هذه المعادلة، وإذا لم تأسر هذه المعادلة لبك، فأنت، وببساطة، لا تملك روحاً. ما تقوم به هذه المعادلة هو أنها تربط بين مفهومين مختلفين كلياً، بين الهندسة المتصلة بالرقم π وبين بساطة الأرقام الفردية. أما النتيجة، فهي ساحرةٌ حقاً ومفاجئة، وتوضح هذه النتيجة، وبدقة، الطريقةَ الغريبة التي تقوم بها الرياضيات بالوصل بين الأنماط المختلفة مع بعضها. كُلما طُلب مني أن أُعرف الرياضيات، فأنا وببساطة أكتب المعادلة \( \frac{ \pi} 4=1-\frac{1}3+\frac{1}5-\frac{1}7+\frac{1}9+ \). وأقول للذين يظنون منكم أن الرياضيات مجرد لغة، فكروا جيداً.
لهذه المعادلة تاريخ رائع. اشتُقت هذه المعادلة في الغرب عام 1671 بواسطة جيمس جريجوري James Gregory من معادلة معكوس ظا(س) [arctan [x، وكذلك اشتُقت بشكل مستقل بواسطة غوتفريد لايبنتس Gottfried Leibniz في وقت لاحق. مع ذلك، اكتُشفت نفس المعادلة (مع نتائج أخرى كثيرة تشتمل على متسلسلات لا منتهية) قديماً من قبل ذلك في القرن الرابع عشر من قِبل الرياضي الهندي العظيم مادافا Madhava. توجد نتائج مشابهة، وذات جمال قريب، وهي المتسلسلة المتقاربة المعطاة بـ
(2)
\(\frac{ \pi^2} 6=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+....\)
و
(3)
\(\frac{ \pi^3} {32}=1-\frac{1}{3^3}+\frac{1}{5^3}-\frac{1}{7^3}+....\)
(4)
و
\(\frac{ \pi^4} {90}=1+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+....\)
ولكن، ولاعتبارات معيّنة، هذه المعادلات مخيبة للآمال؛ ﻷنك إذا احتجت فعلاً أن تحسب \(π\)، أو\( π^2\)، أو \(π^3\)، أو \(π^4\)، فأنت غالباً لن تصل إلى واحدة من هذه المعادلات. والسبب في ذلك أن هذه المعادلات تتقارب بشكل بطيء جداً. إذا أخذت المعادلة رقم (1)، ثم جمعت الارقام حتى 100 حدٍّ، وضربت في 4، سوف تحصل على \(3.146567747182956\)، فبينما يكون هذا الرقم قريباً بشكل معتدل من قيمة \(π= 3.141592653589793\) إلا أنه ليس تقديراً دقيقاً إذا أخذنا بالاعتبار الجهدَ المبذول في جمع 100 حد.
إذا أردت حساب \(π \)، أو \(π2\) لدقة تصل حتى المنزلة العشرية السادسة، ستحتاج أن تجمع حدوداً تصل إلى مرتبة \(10^6 \)(ملايين الحدود) من أيٍّ من المعادلتين (1) أو (2)، وكذلك، وقبل أن تُتِمّ جمعَ كل الحدود في المتسلسلة، فإن أخطاءَ التقريبِ المتعلقةَ بحسابات الحواسيب ستكون تجمعت إلى نقطة تكون عندها دقة الإجابة قد تدهورت بشكل كبير.
العالم يحتاج "پاي"
"ولكن هذا ليس مهماً"، ربما تقول ذلك (أنت وبعض المتخصصين في الرياضيات البحتة). من المؤكد أنك لا تحتاج أن تعرف قيمة \(π\) بهذه الدرجة من الدقة، ففي النهاية، اكتفى الإنجيل بأن يعطينا إياها بدقة مُنزلة واحدة. ولكن \(π\) ليس أي رقم؛ فهو يقع في صميم أي تقنية تتضمن الدوران أو الموجات، وهذا يمثل قسماً كبيراً من الهندسة الميكانيكية والإلكترونية.
إذا لم تُصنع الأجزاء الدوارة، ولنقل في محرك دفع نموذجي بدقة عالية، فإن الأجزاء، وببساطة، لن تعمل. وهذا في العادة يشمل تصحيح القياسات إلى مستوى واحدٍ من \(10^4\)، وكذلك، وﻷن هذه القياسات تشمل \(π\)، فإننا نحتاج أن تكون قيمة \(π\) بهذه الدرجة من الدقة لمنع الأخطاء، فمثلاً، في التصوير الطبي، كما في أجهزة التصوير المقطعي المحوري المحوسب (CAT)، وأجهزة التصوير بالرنين المغناطيسي (MRI)، تتحرك هذه الأجهزة حول حلقة، والتي يجب أن تكون مصنّعة بمستوى دقة واحدٍ من \(10^6\)، الأمر الذي يحتاج دقةً متزايدةً في قيمة \(π\) المستخدمة.
مع ذلك، فإن هذه الدرجة من الدقة تتضاءل أهميتها إذا ما نظرنا إلى الأجهزة الإلكترونية الحديثة، فمثلاً، في الإلكترونيات عالية التردد، والتي تملك ترددات في مستوى 1 جيجا هيرتز (والمتواجد مثالياً في الهواتف النقالة أو تطبيقات نظام التموضع العالمي [GPS])، فإن العلماء عليهم أن يعملوا باستخدام الصيغة \(u(t) = cos(2π ft) \) حيث \(f\sim10^{9}\) ، و t رقم قريب من الواحد. لتحصل على الدقة الموجودة في \(u(t) \)، والتي نحتاجها ليعمل الـ GPS، يجب أن نحصل على دقة بمستوى واحدٍ من \(10^{15}\) لقيمة \(π\) المستخدمة.
وعليه، ولنعيش في عالمنا الحديث، فإننا نحتاج أن نعرف \(π\) بدقة كبيرة. إذاً، ماذا يمكن أن نفعل؟ إحدى الاحتمالات هو أن نأخذ عدداً ضخماً من حدود معادلة \(π\) أعلاه، ونحجز وقتاً طويلاً على حاسب باهض الثمن، ونجلس هناك متكئين وننتظر (ثم ننتظر، وننتظر). أو يمكننا أن نحاول أن نسرع تقاربها (تقارب القيم المحسوبة من المعادلة مع القيمة الحقيقية)، بحيث أنه وبعدد قليل من الحدود (ولنقل 10 حدود)، نستطيع أن نحصل على 10 منازل من \(π\).
الجميل في الموضوع من خلال هذه الطريقة أن اشتقاق المعادلات أمر واضح جداً (وذلك في متناول طالب جامعي من السنة الأولى، أو حتى الطلاب الحائزين على المرتبة A). وبنفس المبدأ، يمكن لهذه الطريقة أن تُستخدَم لإيجاد مجاميع متسلسلات أخرى تكون بطيئة التقارب.
تسريع تقارب متسلسلة
لنفترض أن لدينا متسلسلة
\(a1+a2+a3+a4....+a_n+....\)
ولنعرف المجموع (\(S_n\)) كالتالي
\(s_n=a1+a2+....+a_n.\)
وسنفترض أن هاتين المتسلسلتين تتقاربان. هذا يعني أن هناك مجموعاً مُحددًا (S)، بحيث أن
\(n \to \infty\) as \(S_n \to S\)
فإذا أردنا حساب قيمة S، يمكننا وببساطة أن نأخذ قيم \(S_n\) ونجعل n كبيرة جدًا. ولكن، إذا قمنا فقط بجمع قيم متسلسلة ما، فإن هذا يجعلنا نخسر الكثير من المعلومات المحتواة داخل المتسلسلة، كذلك فإن فعل ذلك يعد أمراً غير لائق. ربما يمكن لنا أن نعصر المزيد من المعلومات من المتسلسلة ونستخدم هذه المعلومات لتسريع تقارب قيم\(S_n\). هذا يعني أن نُضيف حداً تصحيحياً (correction term) إلى معادلة \(S_n\)، بحيث أنها تصل إلى قيمة S بشكل أسرع بكثير. الجميل في هذا الأسلوب، هو أن حساب حدود التصحيح هذه أمرٌ سهل جداً.
لتوضيح هذه الفكرة سنأخذ المتسلسلة (2) المستخدمة لحساب \(\pi^2/6\) . وسنعرف
\(S_n=1+\frac{1}{2^2}+....+\frac{1}{n^2}.\)
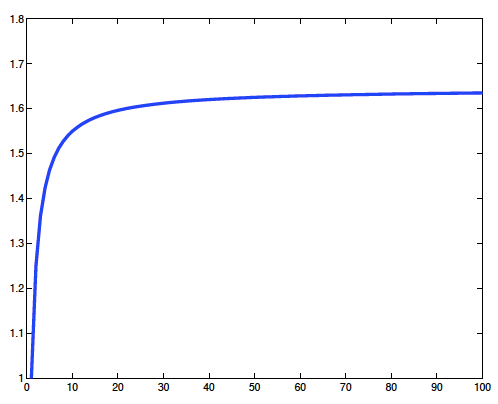
بزيادة n، فإن \(S_n\) تزداد أيضاً بشكل ثابت حتى تقترب من قيمة \(S=\pi^2/6\). في الشكل (1) قمنا برسم قيم \(S_n\) والتي يمكن أن تراها تتزايد حتى تصل قيمة \(\pi ^2/6 = 1.644934066848226. \).
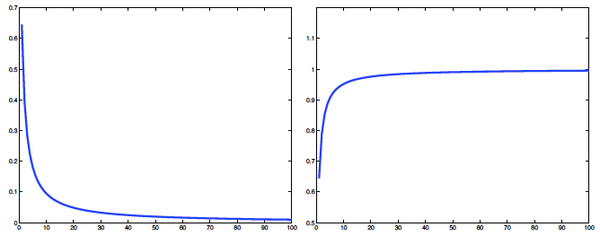
لنفترض أننا سننظر في الفرق \(E_n=s-s_n\). يمكنك أن ترى الرسم في الشكل 2أ، ويمكنك أن ترى أن المنحنى يقلُّ نحو الصفر بزيادة n، ولكن ما هي سرعة هذا النزول؟
ولتقدير بذلك، نقوم برسم قيم \(nEn\) في الشكل 2ب. الواضح من هذه القيم أن \(n \to \infty,nEn\) as \(E \to 0 \) من ثابت ما، والذي يبدو، وبشكل مثير للشك، وكأنه الواحد الصحيح.
من هنا، نستطيع التخمين بأن\(E_n\approx1/n \)، وبالتالي وبمقاربة أولى، نستطيع القول أن:
\(S=S_n+\frac{1}{n}+.....\)
نستطيع تحسين هذا التخمين بأن نفترض وجود سلسلة من الأرقام \(B_0\)، \(B_1\)،\(B_2\)، \(B_3\) … بحيث أن \(∞ → n\).
(6)
\(S=S_n+\frac{B_0}{n}+\frac{B_1}{n^2}+\frac{B_2}{n^3}+\frac{B_3}{n^4}+....\)
إذا استطعنا حساب الحدود التي تحتوي على \(B_r\) لقيم r عندما r = 0, 1, 2, … k، عندها يمكن تقدير قيمة S من معرفتنا لقيمة \(S_n\)، وذلك بوساطة المعادلة:
\(S\approx S_n+\frac{B_0}{n}+\frac{B_1}{n^2}+\frac{B_2}{n^3}+\frac{B_3}{n^4}+....+\frac{B_{k-1}}{n^k}\)
ولكن ما هي قيم \(B_r\)؟
يتضح أن قيم \(B_r\) هي مجموعة من الأرقام المعروفة جداً، وهناك طريقة جميلة ومنظمة لحساب قيمها (ولكن يمكنك تخطي ذلك إلى النتائج مباشرة إذا أردت).
إذا أخذنا المعادلة رقم (6) ووضعنا n-1 مكان n ، سنحصل على:
(7)
\(S\approx S_{n-1}+\frac{B_0}{n-1}+\frac{B_1}{(n-1)^2}+\frac{B_2}{(n-1)^3}+\frac{B_3}{(n-1)^4} +...\)
ومنه نحصل على:
(8)
\( S_{n-1}-S_n=B_0(\frac{1}{n}-\frac{1}{(1-n)})+B_1(\frac{1}{n^2}-\frac{1}{(1-n)^2})+B_2(\frac{1}{n^3}-\frac{1}{(1-n)^3})+...\)
وكذلك، من خلال تعريفنا لـ\(S_n\)، فنحن نعلم أن:
\(S_n-S_{n-1}=\frac{1}{n^2}\)
إذا جمعنا هاتين المعادلتين، نحصل على:
(9)
\(-\frac{1}{n^2}=B_0(\frac{1}{n}-\frac{1}{(1-n)})+B_1(\frac{1}{n^2}-\frac{1}{(1-n)^2})+B_2(\frac{1}{n^3}-\frac{1}{(1-n)^3})+...\)
نستطيع الآن إيجاد قِيَم كلّ حد من حدود \(B_k\) بشكل تكراري عن طريق توسيع كلٍ من هذه المعادلات بقوى 1/n، معتبرين أن قيمة n كبيرة جداً. على سبيل المثال:
\(\frac{1}{(n-1)} =\frac{1}{n(1-1/n)}=\frac{1}{n}+\frac{1}{n^2}+\frac{1}{n^3}+....\)
و
\(\frac{1}{(n-1)^2} =\frac{1}{n^2(1-1/n)^2}=\frac{1}{n^2}+\frac{2}{n^3}+\frac{3}{n^4}+\frac{4}{n^5}+...\)
وبشكل عام:
\(\frac{1}{(n-1)^k} =\frac{1}{n^k(1-1/n)^k}=\frac{1}{n^k}+\frac{k}{n^{k-1}}+.....+\frac { \left( \begin{array}{c} k+r-1 \\ r \end{array} \right) } {n^{k+r}}+...\)
حيث:
\( \left( \begin{array}{c} k+r-1 \\ r \end{array} \right) = \frac {k(k+1)(k+2)+....(k+r-1)} {r!}\)
هذه ما يعرف بـ "مناشير متسلسلة تايلور" للمعادلات أعلاه.
والآن، نستطيع دمج هذه المعادلات مع المعادلة رقم (9). هذا يعطينا
(10)
\(\frac{1}{n^2}=B_0\left( \frac{1}{n^2}+\frac{1}{n^3}+.... \right) +B_1\left( \frac{2}{n^3}+\frac{3}{n^4}+.... \right) + \)
\(+...B_{K-1} \left( \frac {K} {n^{k-1}}+\frac {k(k+1)} {2n^{k+2}}+... + \left( \begin{array}{c} k+r-1 \\ r \end{array} \right) \frac{1}{n^{k+r}} \right) \)
لإيجاد قيمة كل حد من حدود \(B_k\)، نقارن المعادلات المحتويةَ على الصيغة \(1/n^m \) حيث \(m=2,3,4,.....\)، على سبيل المثال، فإن معامل \(\frac{1}{n^2}\) الموجود في الجانب الأيسر من المعادلة أعلاه هو 1، ومعامله على الجهة اليمنى هو \(B_0\).
إذاً:
\(B_0=1\)
وإذا نظرنا بعد ذلك إلى الحدود المحتوية على \(1/n^3\) و \(1/n^4\)، نحصل (بالترتيب) على:
\(1/n^4:0=B0+3B_1+3B_2 \) و \(1/n^3:0=B0+2B_1 , \)
إذا استبدلنا بقيمة \(B_0\) في المعادلة الأولى يعطينا \(B_1\)، وبمعرفة ذلك يمكننا أن نجد \(B_2\) من المعادلة الثانية. من ذلك ينتج:
\(B_2 = \frac {1}{6}\) و \(B_1 =- \frac {1}{2}\)
يمكننا بعد ذلك أن نكمل بشكل استقرائي، ونستطيع استخراج قيم الحدود\(B_K\) من العلاقات المتكررة
(11)
\( B_{k-1}= -\frac{1}{k} \left( \left(\! \begin{array}{c} k \\ 2 \end{array} \!\right) B_{k-2} + \left(\! \begin{array}{c} k \\ 3 \end{array} \!\right) B_{k-3}+....+B_0 \right)\)و\(B_0=1 \)
بتعويض القيم، نحصل على الأرقام التالية
(12)
\(B_4=-\frac{1}{30},\) \(B_3=0,\) \(B_2=\frac{1}{6},\) \(B_0=1,B_1=-\frac{1}{2}, \)
\(B_9=0,.....\) \(B_8=-\frac{1}{30},\) \(B_7=-0,\) \(B_6=\frac{1}{42},\) \(B_5=0,\)
نلاحظ أنه إذا كانت k عدداً فردياً أكبر من الواحد، تكون \(B_K=0,\)، وأن قيم \(B_K\) تختلف في الإشارة. الأرقام التي حسبناها صغيرة جداً، ولكنها تزداد (وبشكل سريع) بزيادة k. على سبيل المثال:
\(B_{50}=\frac {495057205241079648212477525}{66}\)
تعتبر هذه الأعداد شائعة، ويطلق عليها "أعداد بيرنولي" (Bernouli numbers). تَظهر هذه الأعداد في كل مكان، بدءاً من "نظرية الأعداد" وحتى الميكانيكا وما وراءها. وصف جاكوب بيرنولي هذه الأعداد في الكتاب Ars Conjectandi (والذي نُشر بعد وفاته، عام 1713) مع مواضيع متعلقة بمجاميع قوى الأعداد الصحيحة، كما أن عدداً من علماء الرياضيات الآخرين اكتشفوها بشكل متزامن تقريباً.
منذ ذلك الحين، وهذه الأعداد تلعب دوراً مهماً في تاريخ الرياضيات؛ فعلى سبيل المثال، تعتبر هذه الأرقام مهمة جداً في فهم "مبرهنة فيرمات الأخيرة"(Fermat's last theorem)، و"دالة زيتا لريمان" (Riemann zeta function)، وقد صُمِّم أول برنامج حاسوبي، والذي كتبته "آدا لوفيليس" Ada Lovelace في 1842، ليحسب هذه الأعداد.
القيام بعملية جمع سريعة
تلخيصاً لما سبق، لكل قيمة ثابتة من n و k، يمكننا إضافة n من الحدود في المتسلسلة الأصلية لنجد\(S_n\)، ومن ثم نضيف k من حدود المتسلسلة التالية:
(13)
\(E_{n,k}= \frac {B_0} {n}+ \frac {B_1} {n^2}+.....+ \frac {B_{k-1}} {n^k}\)
لنحصل على التصحيح. نستطيع بعدها أن نُقدر قيمة S عن طريق
\(S\approx S_n+E_{n,k}\)
أما نسبة الخطأ بين هذه المقاربة وبين قيمة S، فإنها تُعطى (بشكل تقريبي) عن طريق الحدّ التالي في المتسلسلة\(E_{n,k}\) ، والذي يُعطى عن طريق \(B_{k+1}/n^{k+1}\) على سبيل المثال، إذا كان n=k=10، فإن
(14)
\(S=S_n+\frac {1}{n}-\frac {1}{2n^2}+\frac {1}{6n^3}-\frac {1}{30n^5}+\frac {1}{42n^7}-\frac {1}{30n^9}+o \left( \frac {1} {n^{11}} \right) \)
حيث يوضح الحدُّ الأخير حقيقة أن نسبة الخطأ التي نتوقعها تتناسب مع \(1/{n^{11}}\). لكل n=10 حدود، هذا سيعني أن نسبة خطأ بقيمة \(10^{-11}\)، وهذا يعتبر تحسيناً ملحوظاً إلى نسبة خطأ بقيمة 0.1 والتي كنا لنحصل عليها إذا أضفنا حدود المعادلة بشكل ساذج.
إذاً ما هي المشكلة في عمل ذلك؟ حسناً، المشكلة في هذا الأسلوب هو أنه كلما تزداد أعداد بيرنولي \(B_k\) سريعاً بزيادة k، فإن "حد التصحيح" سيصبح كبيراً جداً في النهاية. في الحقيقة، فإنه إذا كانت n "ثابتة"، فإن كل حدٍ من حدود \(E_{n,k}\) سيقترب من اللا نهاية كُلما \(K \to \infty \).
للحصول على "نسبة خطأ مُثلى" لقيمة معطاة لـn، فإن الطريقة الأمثل تكون بقطع (to truncate) متسلسلة التصحيح وأن نأخذ k=n، مقدِّرين قيمة S عن طريق \(S+E_{n,n}\). هذا يعطي نسبة خطأ تتناسب مع \(1/n^n\).
نستطيع لعب نفس هذه اللعبة مع المتسلسلات الأخرى المذكورة في هذه المقالة.
هل هذا جيدٌ كفاية؟
نعم، هو جيد جداً! لنرَ ذلك علينا أن ننظر إلى جدولٍ من قيم \(S_n\) لقيم n=1, 5, 10، ومن ثم إلى التصحيحات الثلاثة المعطاة عن طريق
\(P_n=S_n+\frac{1}{n}\)
\(Q_n=S_n+\frac{1}{n}-\frac{1}{2n^2}+\frac{1}{6n^3},\)
\(R_n=S_n+\frac{1}{n}-\frac{1}{2n^2}+\frac{1}{6n^3}-\frac{1}{30n^5}+\frac{1}{42n^7}-\frac{1}{30n^9}\)
| n | \( S_n\) | \(p_n\) | \(Q_n\) | \(R_n\) |
| 1 | 1 | 2 | 1.666666666666667 | 1.623809523809524 |
| 5 | 1.463611111111111 | 1.663611111111111 | 1.644944444444445 | 1.644934065473016 |
| 10 | 1.549767731166541 | 1.649767731166541 | 1.644934397833208 | 1.644934066847493 |
نستطيع أن نرى أن المقاربة \(R_{10}\) هي مقاربة جيدةٌ جداً لقيمة \(\pi^2/6=1.644934066848226\)، بنسبة خطأ بقيمة \(7×10^{-13}\). هذا الأمر مذهل بشكل خاص عندما نرى أن \(S_{10}\) مقاربةٌ ضعيفة جداً لقيمة \(\pi^2/6\). لاحظ أننا احتجنا هنا ﻷن نضيف 6 حدود إضافية فقط للحصول على ذلك. للحصول على نفس هذه الدقة من استخدام متسلسلة \(S_n\)، كان يتوجب علينا أن نضيف \(10^{11}\) من الحدود! يمكنكم أعزائي القراء أن تحسبوا قيمة\(S_{10}\) و \(R_{20}\) لتروا الدقة المذهلة لهذه الطريقة.
هل هذا الأمر جديد؟
إطلاقاً. الفكرة الأساسية في تسريع تقارب متسلسلة ما تعود إلى عالم الرياضيات الفذ "ليونهارت أويلر" Leonhard Euler، أو حتى ربما اكتُشفت قبله. مواجهاً "متسلسةً متناوبةً" كالمتسلسلة الأولى (1) التي عاينّاها لحساب قيمة \(\pi/4\)، حيث تتناوب الحدود في إشارتها، فإن أويلر صمم تحويلاً ما، بحيث لا يقوم بجمع حدود المتسلسلة، وإنما قام بجمع "الفروق المقسومة" لهذه المتسلسلة.
هذه الطريقة لا تصلح للمتسلسلات ذات الحدود الموجبة، كما في المتسلسلة (2) والتي استخدمناها لحساب \(\pi^2/6\). ولكن أويلر احتاج أن يجد مجموع هذه المتسلسلة، ذلك أن مجموعها لم يكن معروفاً في ذلك الوقت (1735). ظهرت قضية إيجاد هذا المجموع (وإيجاد دليل عليه) عام 1644، وقد حاول العديد من علماء الرياضيات المشهورين إيجاد حلٍ ما، لكنهم فشلوا. كانت فكرة أويلر هي مقارنة مجموع الحدود ذات الصيغة \(1/n^2\) مع تكامل الدالة \(1/x^2\). كما كان معهوداً في ذلك الوقت.
\(\int \frac {dx} {x^2}=-\frac{1}{x}+c\)
كما أن مجموع الحدود \(1/n^2\) يعتبر تقريباً لقيمة هذا التكامل. إذا كان بإمكانك إيجاد نسبة الخطأ في هذه التقريب، فإنه يمكنك إيجاد مجموع المتسلسلة عن طريق مقارنتها بالتكامل المعروف. في عمله المشهود له بالتميز (كما هو حال أعماله)، فإن أويلر استطاع حساب نسبة الخطأ هذه، مشتقاً بذلك "متسلسلة أويلر-ماكلورين التباعدية" (المشهورة حالياً) لنسبة الخطأ هذه.
إذا أخذت n من الحدود من المتسلسلة الأصلية للمجموع، وأخذت k من الحدود من متسلسلة أويلر-ماكلورين، فإنك تحصل على المعادلة رقم (13) التي اشتققْناها. إنه أمر مُفرح (لمحلل عددي مثلي) أن يضع في اعتباره أن أويلر استخدم معادلته ليحسب المجموع الناتج من المتسلسلة (2) بشكل صحيح حتى عشرين خانة عشرية (بالطبع بدون الاستفادة من أي شكل من أشكال الحاسبة). كان أويلر قادراً (من خلال حساباته) أن يُخمن أن مجموع هذه المتسلسلة هو \(\pi^2/6\). بمعرفة النتيجة، كان أويلر قادراً على إيجاد الدليل.
أُعيدت تسمية المعضلة إلى "معضلة بازل" (Basel Problem) تكريماً لمسقط رأس كل من أويلر وعائلة برنولي (والذين هاجموا المعضلة بشكل غير مبرر)، وانتشرت شهرة أويلر (وهو بسن 28 عاماً فقط) مدى الحياة.
بهذه الطريقة الهجومية، توقّع أويلر من الرياضيات الحديثة، والتي يُستخدَم فيها الحاسب كأداة تجريبية، أن تحصل على تبصُّرٍ في هذه المسألة، كمرحلة أولى لإثبات النتيجة. في هذه الأيام، نستخدم هذه الطريقة طوال الوقت، والتي يستمر الوثوق بها كونها تقوم بحسابات عالية الدقة. ولكن الأمر اللطيف حول التقنيات التي وصفتُها في هذه المقالة، هو أننا نستطيع رؤية أنه إذا قمنا ببعض العمليات الرياضية الإضافية، فبإمكاننا الحصول على نتائج أفضل بكثير من أفضل الحواسيب.