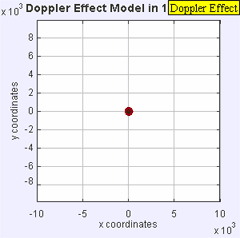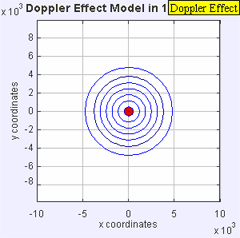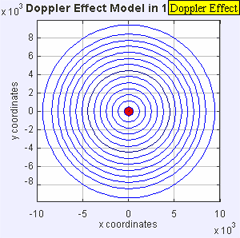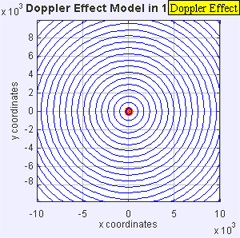
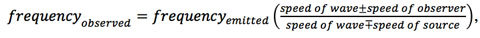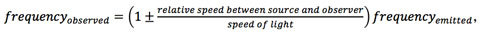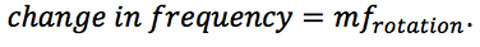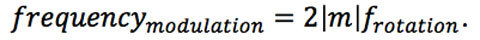لدينا عدد من الأجهزة لنقيس سرعة جسمٍ ما. نقيس النجوم المتحركة والمجرات والحشرات وكرات البيسبول، وربما الأكثر شيوعاً هو ضبط سيارةٍ متجاوزةٍ للسرعة القانونية على الطريق السريع، لكن هذه الأجهزة تستعمل نفس المبدأ الذي يستعمله العلماء لقياس السرعة التي تتحرك بها الأجرام السماوية، ألا وهو تأثير دوبلر الخطي linear Doppler effect.
يمكن لتأثير دوبلر أن يساعد على التنبؤ بالطقس، وكذلك تصوير الأجنة في الأرحام. مؤخراً، حصل تأثير دوبلر الزاوي angular Doppler effect الذي يستعمل لقياس السرعة الدورانية على مزيدٍ من الاهتمام.
الكثير من الأشياء تدور حول محور ما، كالكواكب والنجوم والمجرات وأقراص الدي في دي وكرات البيسبول والعجلات والقمم والأعاصير والذرات وأكثر. يمكن للقدرة على قياس خصائص الدوران أن تعطينا نظرةً على بنية هذه الأشياء، وكشف بحثٌ نُشر في آب/أغسطس من العام 2013 عن بعض الاكتشافات الجديدة فيما يخص انزياح دوبلر الدوراني.
تأثير دوبلر الخطي
يحدث تأثير دوبلر الخطي عندما يكون لمصدر الموجة وملاحِظها (راصدها) حركة خطية متناسبة فيما بينهما. ومن المهم أيضاً ملاحظة وجود فروق طفيفة بين حركة مصدر الموجة باتجاه الراصد وحركة الراصد باتجاه مصدر الموجة.
على سبيل المثال، سماع شخص ثابت لصوت صفارة سيارة الإسعاف، حيث سيسمع زيادةً في التردد كلما اقتربت الصفارة ونقصاناً في التردد كلما ابتعدت. هذا لأن الموجات الصوتية المنبعثة من الصفارة تنبعث من نقاط قريبة من الراصد عندما تقترب الصفارة منه، ومن نقاط بعيدة عنه عندما تبتعد الصفارة.
في هذه الحالة، لا يلمس الراصد أي تغير في سرعة الموجة. يلمس الراصد طولاً موجياً أقصر وتردداً أكبر في حالة الاقتراب، وطولاً موجياً أطول وتردداً أصغر في حالة الابتعاد. سيستقبل راكبٌ ضمن سيارة الإسعاف المتحركة مقدمة موجية ثابتة من الصفارة ولن يرصد أي تغير في التردد.
 يُظهر هذا المخطط كيف يبدو تأثير دوبلر بالنسبة لملاحِظ تمر به سيارة إسعاف تدوي صفارتها.
|
 يُظهر هذا المخطط الموجات المنبعثة من مصدر ثابت. مصدر الصورة: lookang via Wikimedia commons.
|
عندما يتحرك الراصد ويبقى مصدر الصوت ثابتاً، عندها لا تتغير المسافة بين مقدمات الموجة المنبعثة من المصدر. بدلاً من ذلك، يتحرك الراصد عبر هذه الموجات ويظهر له أن الموجة هي التي تتحرك بسرعة أكبر وتردد أعلى.
يلحظ الراصد المتحرك مقدمات الموجات بمعدل أكبر عند الاقتراب (تردد أعلى)، وبمعدل أصغر عندما يبتعد الراصد عن المصدر (تردد منخفض).
هذه المعادلة التي توضح تأثير دوبلر الخطي للموجات التي لا تتحرك بسرعة كبيرة (أقل بكثير من سرعة الضوء):
حيث العلامات العليا -زائد في البسط وناقص في المقام- تستعمل في الحركة المقتربة، والعلامات السفلى في الحركة المبتعدة. ولا تأخذ هذه المعادلة بعين الاعتبار حركة الوسط.
إذا كانت هناك حركة نسبية بين مصدر يتفاعل مع جسم عاكس (مثل جدار)، فالموجة المُحدثة والمنعكسة تُزاح بشكل متردد منتجةً تردداً أعلى يُكشَف إذا كان الشيء العاكس يتحرك باتجاه الكاشف، وأدنى إذا كان يبتعد.
يساعد الوقت الذي تستغرقه الإشارة للوصول إلى الكاشف في تصوير السطح العاكس للإشارة، ويقدم تغير التردد معلومة حول كيفية تحرك هذا السطح. ويستعمل هذا في إنشاء صور بالموجات فوق صوتية ولتقديم معلومة حول الحركة، ويستخدم لتصوير تدفق الدم وحركة العضلات والأجنة داخل الرحم.
يظهر تردد الضوء عالياً (انزياح نحو الأزرق) عندما يتحرك جسم نحو الراصد، وأدنى (انزياح نحو الأحمر) عندما يتحرك بعيداً عنه.
يرى الفلكيون طيف نجم ما ويثبتون سطوعه الحقيقي ومن ثم يقيسون سطوعه الظاهري، وبالمقارنة بين السطوع الظاهري والحقيقي، يمكننا معرفة كم يبعد عنا ذلك النجم. بالنسبة للمجرات، ينظر الفلكيون إلى نجوم داخل المجرة لتقدير بعد المجرة عنا. من خلال قياس كيفية ازياح تردد الضوء، يمكن للفلكين تحديد فيما إذا كان النجم يقترب أو يبتعد عنا وسرعة اقترابه أو ابتعاده. أظهر هابل Hubble من خلال قياساته أن هناك علاقة خطية بين مسافة وكمية انزياح التردد، وتدعى هذه العلاقة بقانون هابل (Hubble’s law).
بمعرفة سطوع نجم ما يمكن معرفة بعده، ومن هناك يمكن معرفة بعد المزيد من المجرات بمعرفة كيفية انزياح ترددها وباستعمال قانون هابل.
الضوء مقابل الصوت
تختلف الموجات الضوئية عن الموجات الصوتية لأنها لا تتطلب أي وسط لتنتقل عبره. كما تعتبر سرعة الضوء الحد الأعلى للسرعة في فهمنا الحالي للفيزياء المرتكزة على النسبية الخاصة. أما بالنسبة للضوء أو أي إشعاع كهرومغناطيسي، فلا يمكننا التمييز إن كان المصدر هو الذي يتحرك أم الراصد، ويقودنا ذلك إلى الوصف الرياضي التالي:
حيث نستعمل إشارة الزائد عندما يتقارب المصدر والراصد، وإشارة الناقص في حالة التباعد. إذا كان الضوء في تفاعل مع جسم عاكس -مرآة متحركة على سبيل المثال- عندها يتضاعف انزياح التردد.
هذا الفيديو حول مبادئ تأثير دوبلر الخطي.
ملاحظة: تبين نهاية الفيديو أن كل المجرات في انزياح نحو الأحمر (تبتعد عن بعضها البعض). معظمها كذلك لكن ليس كلها، فعلى سبيل المثال، مجرة المرأة المسلسلة أندروميدا هي في انزياح نحو الأزرق (تتحرك نحونا) ويتوقع أن تصطدم بمجرتنا خلال 4 مليار سنة.
مع الالتواء
أولاً، من المهم التنويه بأنه إذا لم يكن للضوء أي جزء زاوي، لا يحدث أي انزياح زاوي للتردد. يعتبر الجزء الزاوي الذي نأخذه بعين الاعتبار عادةً أنه آتٍ من الاستقطاب الدائري للضوء أو أي موجة كهرومغناطيسية.
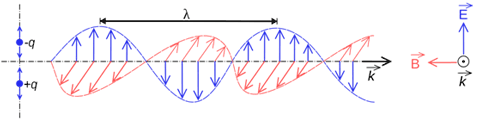
تتكون موجات الضوء من حقل كهربائي وآخر مغناطيسي متعامدان بالنسبة لبعضهما البعض وينتقلان عبر الفضاء. إذا كان الحقلان الكهربائي والمغناطيسي يدوران حول الاتجاه الذي ينتقلان به، عندها يكون الضوء مستقطباً دائرياً. يبدو الضوء المستقطب خطياً مثل مخطط الموجة الكهرومغناطيسية في الأسفل.
الضوء المنعكس عن الماء أو الزجاج هو مستقطب خطياً بشكل جزئي، أو مستقطب كلياً بزاوية معينة تسمى (زاوية بروستر) Brewster angle. تمنع النظارات الشمسية المستقطبة مرور استقطاب (أو اتجاه) واحد للضوء وبالتالي التقليل من الضوء الكلي الواصل للعين.
إن انزياح دوبلر الزاوي أو الدوراني موجود منذ فترة من الوقت. في المرجع 2، هناك اشتقاق لانزياح تردد دوبلر الزاوي. يقدم الجدول أدناه مقارنةً بين تأثيري دوبلر الخطي والزاوي على مصادر الضوء، مأخوذة من المرجع 2.
| تغير في التردد ملاحظ، لا تفاعل مع الجسم العاكس | تغير في التردد ملاحظ، يتفاعل الضوء مع الجسم العاكس (مرآة متحركة مثلاً) | |
| تأثير دوبلر الخطي | ± تردد (دوران) (السرعة النسبية/سرعة الضوء) | ± 2 تردد (دوران) (السرعة النسبية/سرعة الضوء) |
| تأثير دوبلر الزاوي (بالنسبة لمصدر ضوئي مستقطب دائرياً) | ± تردد (دوران) | ± 2 تردد (دوران) |
على سبيل المثال، إذا كان مصدر الضوء يدور فإن التردد المرصود ينزاح بواسطة تردد الدوران، أو ± تردد (دوران). عندما ينعكس الضوء المستقطب دائرياً عن مرآة تدور، ينزاح ترددها بـ ± 2 تردد (دوران). إذا لم يكن الضوء مستقطباً دائرياً فلا يوجد تردد منزاح مرصود في هذه التوصبفات.
نتائج جديدة
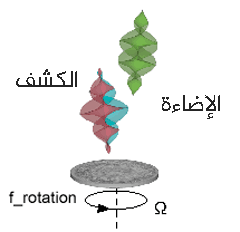
في آب/أغسطس من العام 2013، نشر فريق بحث اسكتلندي نتائج مهمة تتضمن تأثير دوبلر الزاوي. بدلاً من استخدام الضوء المستقطب دائرياً، استعمل الباحثون ضوءاً ينتقل إلى الأمام بشكل حلزوني أو لولبي، حيث تحمل موجة الضوء الحلزونية معلومات زاوية حول كيفية توزع الضوء في الفضاء.
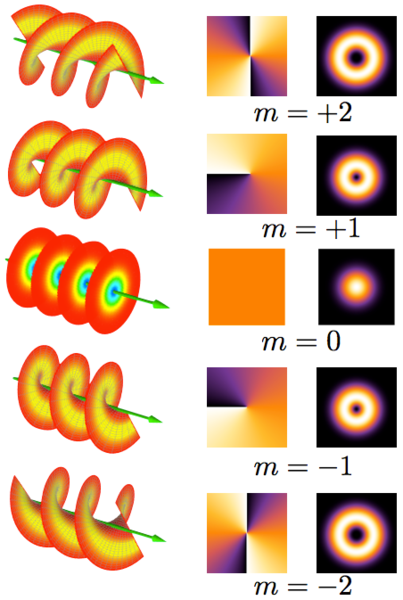
يشير الوضع m إلى عدد الالتواءات، وإلى الاتجاه الذي يصنعه دوران الضوء مع اتجاه الانتشار.
- من أجل الوضع m=0 الضوء ليس حلزونياً، بل يتكون من دوائر غير متصلة على شكل موجة مستوية.
- من أجل الوضع m=+1، الضوء بشكل سطح حلزوني وحيد يلتف مرة واحدة عكس اتجاه عقارب الساعة عندما ننظر إليه من الأمام خلال طول موجي واحد.
- من أجل الوضع m=-1 يلتف مرة واحدة في نفس اتجاه عقارب الساعة خلال طول موجي واحد.
- من أجل الوضع m=+2 يشكل الضوء سطحين حلزونيين في طول موجي واحد.
لأخذ فكرة عن هذا، تتبع المسارات الحلزونية الداخلية والخارجية في الصور أعلاه من m=-1 إلى m=-2.
وجد العلماء أنه عند تفاعل الضوء الحلزوني مع سطح قاسٍ يدور، فإن انزياح التردد المرصود يتعلق بالوضع m الخاص بموجة الضوء الحلزونية.
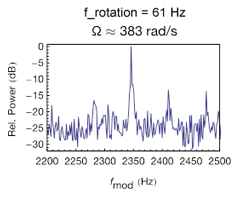
عندما استعمل الباحثون شعاعين حلزونيين لوضعين مختلفين (±M) يصدران الضوء على جسمٍ قاسٍ يدور، لوحظ تغير في الشدة في التردد، مع شدة نسبية متزايدة (قوة في وحدة مساحة) عند تردد يعادل:
يعني السطح القاسي أن الضوء الوارد ينعكس بعدة اتجاهات وأوضاع مختلفة. استعمل الباحثون السطح القاسي لضمان أنه بغض النظر عن الأوضاع التي يحتويها مصدر الضوء الوارد، فإن الضوء المبعثر سيحتوي على عدد أكثر من الأوضاع m. جرب العلماء المعادلة من أجل تعديل الشدة للتردد بأوضاع مختلفة ووجدوا نتائج تدعم المعادلة في الأعلى.
 تتبعثر الأشعة الواردة من الأشكال الحلزونية المعاكسة (أخضر) عن سطح يدور، حيث يكون الشعاع بوضع m سالب منزاحاً نحو الأحمر، أما m موجب فيكون منزاحاً نحو الأزرق.
|
 ينتج عن ذلك شدة نسبية متزايدة في تردد دوبلر منزاح متعلق بالوضع. الشدة النسبية هي القوة النسبية في وحدة المساحة. مصدر الصورة: Martin Lavery, University of Glasgow
|
بعدها عكس العلماء تجربتهم بتبديل المصدر والكاشف واستطاعوا الحصول على أدلة تجريبية تدعم مرة أخرى العلاقة مع معادلة تعديل التردد. بالاعتماد على نتائجهم، أظهر الباحثون أنه بإمكانهم استنتاج تردد دوران جسم بعيد بالأخذ بعين الاعتبار تعديل شدة تردد المرصود.
ما التالي؟
ذكر العلماء مجالين للتطبيق في مقالهم، وهما الاستشعار عن بعد لاضطراب ضوء الأشعة المرتدة والكشف عن بعد عن دوران الأجرام السماوية كمعدل دوران كوكب خارج المجموعة الشمسية على سبيل المثال.
