المفهوم الفيزيائي
يصف تأثير أو انزياح دوبلر كيف يتغير تردد الموجات عندما يتحرك المصدر والراصد بحركة نسبية، ويعطى انتقال تردد دوبلر في السرعات الصغيرة للراصد أو المصدر بالنسبة لسرعة الموجة، بالعلاقة التقريبية التالية:
\(\frac{\Delta f}{f}=\frac{\Delta \nu }{c} \)
حيث :Δv السرعة النسبية بين المصدر والراصد على طول الخط الذي يجمعهما، مع قيمة موجبة عندما يقترب المصدر والراصد وقيمة سالبة عندما ينفصلان.
Δf: هو التغير في التردد.
C: هي سرعة الموجة.
F: التردد الغير المزاح للموجة الصادرة.
انزياح دوبلر في المستوى أحادي الأبعاد
عندما يتحرك المصدر والراصد في أتجاه بعضهما البعض، يزداد التردد الظاهري للموجة. وعندما يتحرك المصدر والراصد متباعدين عن بعضهما البعض يبدو تردد الموجة وكأنه يتناقص.
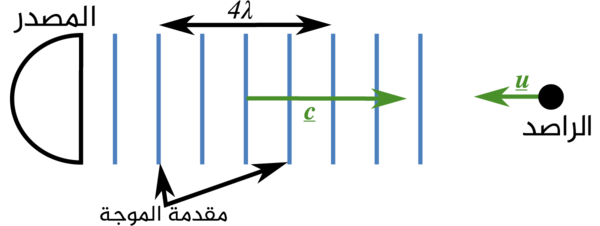
من أجل توضيح ذلك لنتخيل وضعين مختلفين. الأول، نأخذ بالاعتبار مصدر ثابت مع راصد متحرك، يتجه الراصد نحو المصدر بسرعة u يصدر المصدر صوتاً في الهواء بطول λ، والتي هي المسافة الفيزيائية بين مقدمات الأمواج. التردد المقاس عندها هو المعدل الذي يعبر فيه الراصد مقدمات الأمواج. وإذا كان الراصد ثابت هذا يعني:
\(\lambda =\frac{c}{f} \)
من معادلة الموجة، c هي سرعة الموجة وf هو التردد الصادر من الموجة. لراصد يتحرك بسرعة u باتجاه مصدر ثابت ستصل الموجة بسرعة تساوي \(c+u\)، المسافة بالنسبة للراصد بين مقدمات الأمواج تظل λ، وبذلك تصبح معادلة الموجة:
\(\lambda =\frac{c+u}{\nu} \)
وبما أن المسافة بين مقدمات الأمواج λ لا تتغير، لذا يمكن مساواة هاتين المعادلتين كالتالي:
\(\lambda =\frac{c+u}{\nu}=\frac{c}{f} \)
\(\nu =f(1+\frac{u}{c}) \)
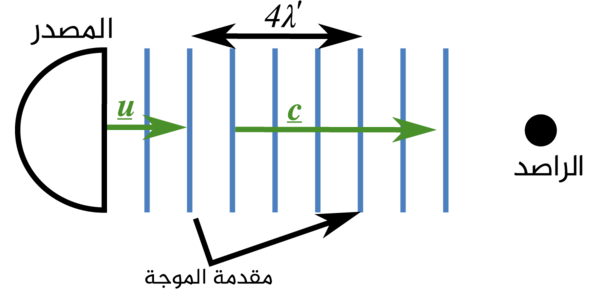
ولكن سينقص الطول الموجي، هذا لأنه في إطار المصدر يتم اصدار مقدمات الموجة عند المعدل ذاته للمصدر الثابت، ولكن عند الزمن الذي يتم إصدار مقدمات الموجة فيه، يكون المصدر قد تحرك، لذلك في هذه الحالة تكون كل مقدمة موجة أقرب إلى سابقتها بالمقارنة مع حالة انعدام الحركة.
يمكن إيجاد النقصان في λ من خلال أخذ المسافة بين المصدر وآخر مقدمة بينما تصدر المقدمة التالية. عند هذه النقطة يكون قد مر زمن 1/f وآخر مقدمة موجية تبتعد عن المصدر بسرعة نسبية c-u هذا يعني المسافة التي قطعتها قبل اصدار المقدمة التالية وهي الطول الموجي الجديد \(λ′\) ويساوي:
للراصد الساكن، تتحرك هذه الأمواج بالسرعة c، بطول موجي \(λ′\)، هذا يؤدي إلى علاقة جديدة ل \(λ′\):
\(λ′ =\frac{c}{v}\)
\(ν =\frac{f}{1-\frac{u}{c}}\)
من كلا المعادلتين اللتين قمنا باشتقاقهما، حيث u صغيرة بالمقارنة مع C ، باستخدام توسع ذو حدين في الحالة الثانية يمكن أن يتبين لدينا:
\(\frac{Δf}{f}=\frac{Δv}{c}\)
تتشابه الحالتان عندما تكون u<<c، حيث أمثلة المصدر والراصد المتحركان تعطي نتائج مشابهة. ولكنهما يختلفان عند السرعات العالية. يمكن أن يلحق المصدر المتحرك بالموجات الصادرة، وأيضا عندما تقترب u من c يميل التردد المرصود إلى اللانهاية-يؤدي هذا إلى ظاهرة تعرف بدوي اختراق حاجز الصوت sonic boom. بالنسبة للراصد المقترب، يتضاعف التردد المرصود عندما تقترب u من c.
سؤال سريع
ما هو التغير التقريبي في التردد لصفارة سيارة ترددها 440 Hz من قبل راصد ثابت لمح السيارة تتحرك بسرعة 20 م/ث؟ سرعة الصوت في الهواء c=340 م/ث
- الجواب
\(Δf=\frac{f Δv}{c}\)
بتعويض الرقم يعطي هبوط في التردد بمقدار 26Hz.
انزياح دوبلر على الأمواج الكهرومغناطيسية
يختلف الاشتقاق في الأمواج الميكانيكية، ويعطي نتيجة لا تعتمد على إذا ما كان المصدر أو الراصد هو الذي يتحرك. فالحركة عند سرعة u على طول الخط الذي يجمع المصدر والراصد، عندما تكون u<<c تكون النتيجة التقريبية:
\(\frac{Δf}{f}=\frac{u}{c}\)
مثلها مثل الموجات الميكانيكية.
انزياح دوبلر في المستوى الثنائي والثلاثي الأبعاد
يمكن أن يمتد انزياح دوبلر ليصف المصادر في جميع الأبعاد. من أجل حساب انتقال دوبلر في هذين البعدين يتم استخدام نفس المعادلة. ولكن، بدلاً من \( |\Delta \veebar|\) علينا الآن اعتبار التغير في السرعة في اتجاه الراصد: \(|\Delta \veebar | cosθ \) حيث θ هي الزاوية بين شعاع السرعة النسبية Δv وشعاع الموضع النسبي\( \bar{x}\) هذا يعطي الانزياح بالمعادلة التالية:
\(\frac{\Delta f}{f}=\frac{\Delta \veebar }{c} cosθ \)
كما سبق، إذا كان الراصد والمصدر يبتعدان عن بعضهما البعض، علي سبيل المثال تكون نسبية للمصدر أوالراصد، هناك مكون زاوي للسرعة الموجهة بعيداً، عندها نأخذ Δv ليكون سالباً. ولـ θ=0 نعود لمعادلتنا الأصلية.
واقتباساً من الفلكي جون دوسون John Dobson "سبب انزلاق الصفارة لأنها لا تصطدم بك"، هذا يعني أنه إذا كان هناك جسم يتحرك باتجاهك مباشرة، عندها θ=0 ولا تتغير. مما يعني أنه عندما ينزاح الصوت، فإنه ينزاح بمقدار ثابت. ولكن إذا لم يكن الجسم يتحرك باتجاهك مباشرةً، عندها ستتغير θ بين 0 و 90 درجة، وسيكون مقدار انزياح دوبلر يتغير عندما تتغير الزاوية، مما يؤدي إلى انزلاق الصفارة عند تغير θ.
سؤال
سيارة إسعاف تتجاوز سيارة ساكنة، تتحرك سيارة الإسعاف بسرعة 45 م/ث وهي أما أمام ويمين السيارة بخمس أمتار، وصفارتها تضج بتردد 440 Hz وسرعة الصوت 340 م/ث ، ما هو التردد الذي يسمعه الناس داخل السيارة؟
- الجواب
\(\nu=f(1-\frac{u}{c}cos\theta )=400Hz \)