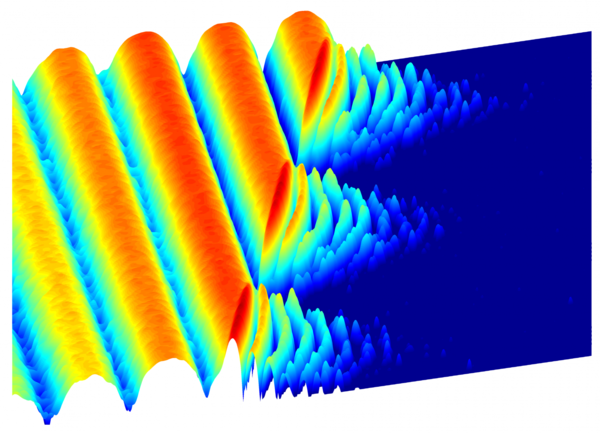
الضوء كطبيعة موجية ومادية
حقوق الصورة: Fabrizio Carbone/EPFL
ستة أشياء عليك معرفتها عن فيزياء الكم
جرت العادة على تهويل الفيزياء الكمية منذ بداياتها، إنها ضرب من الغرابة ويمكن أن تبدو غير بديهية، حتى بالنسبة للفيزيائيين الذين يتعاملون معها يومياً . لكنها ليست عصية على الإدراك، إذا كنت تقوم بقراءة شيء ما عن الفيزياء الكمية، هناك عملياً ستة مفاهيم أساسية حولها عليك أن تضعها في اعتبارك، افعل ذلك، وستجد أن الفيزياء الكمية يمكن فهمها بشكل أسهل.
- كل شيء له طبيعتان: مادية وموجية
هناك العديد من الأماكن التي يمكن بدء هذا النوع من النقاش منها، وهذا جيد كأن نبدأ من: لجميع المواد في الكون طبيعة موجية وطبيعة مادية، في نفس الوقت، هناك سطر في ثنائية غريغ بير Greg Bear الخيالية ( الكونشيرتو اللانهائي (The Infinity Concerto والساحر ماجي The Serpent Mage)، حيث تقوم إحدى الشخصيات بوصف أساسيات السحر بالقول: "كل ما هنالك هو أمواج، مع عدم وجود أي شيء ليتموج على أي مسافة على الإطلاق."
لطالما أحببت ذلك كوصف شاعري للفيزياء الكمية، - في العمق، كل شيء في الكون له طبيعة موجية طبعاً، كل شيء في الكون لديه طبيعة مادية أيضاً. يبدو ذلك ضرباً كاملاً من الجنون، ولكنه واقع تجريبي، تم استنباطه من عمليات مألوفة لدرجة مثيرة للدهشة.
بالطبع، وصف الأجسام الحقيقية بالمادية والموجية غير دقيق بالضرورة، بطريقة ما. ينبغي القول، الأجسام التي يتم وصفها بالفيزياء الكمية هي ليست ذات طبيعة موجية ولا طبيعة مادية، ولكنها تندرج تحت فئة ثالثة تشترك ببعض الخصائص مع الأمواج (طول موجة وتردد مميز لها، وانتشار ما في الفراغ)، وبعض خصائص الجسيمات المادية (هذه الأجسام عموماً قابلة للعد، ويمكن تحديد مكانها إلى درجة ما).
وهذا يقود إلى نقاش حيوي داخل مجموعة تعليم الفيزياء حول ما إذا كان من المناسب حقاً الحديث عن الضوء كمادة في مناهج الفيزياء الدراسية؛ لا يعود ذلك إلى وجود أي جدل حول ما إذا كان للضوء طبيعة مادية نوعاً ما، ولكن تسمية الفوتونات بالجسيمات بدلاً من أن تسمى "إثارة لحقل كمومي" يمكن ان تؤدي إلى سوء فهم لدى بعض التلاميذ. لا أميل إلى قبول ذلك، لأن العديد من نفس المسائل التي يمكن أن تثار حول الطبيعة المادية للإلكترون هي فقط لإيجاد منشأ واقعي لنقاشات على شبكات التواصل.
هذه الطبيعة "الباب رقم ثلاثة" للأجسام الكمومية تنعكس في اللغة المضطربة التي يستخدمها الفيزيائيون أحياناً للتعبير عن الظاهرة الكمومية. اكتُشف بوزون هيغز Higgs boson كجزيء (جسيم) في مصادم الهادرونات الكبير Large Hadron Collider، ولكن ستسمع الفيزيائيين يتحدثون عن "حقل هيغز" Higgs field كشيء عديم التموضع يملأ الفراغ كله.
يحدث ذلك لأنه في بعض الحالات، مثل تجارب المصادم، من المناسب أكثر مناقشة الإثارات الخاصة بحقل هيغز بطريقة تؤكد على خصائصه المشابهة للجسيمات، بينما في حالات أخرى، كالنقاش العام لسبب امتلاك بعض الجسيمات لكتلة، من المناسب أكثر مناقشة الفيزياء من حيث التفاعلات مع حقل كمومي يملأ الكون، إنها فقط مجرد لغة مختلفة لوصف نفس الجسم الرياضي.
- فيزياء الكم غير مترابطة
هذه التذبذبات خلقت صورة مجمدة للضوءحقوق الصورة: Princeton
ذلك صحيح اسمياً- الكلمة "كمّ" "quantum" تأتي من المرادف اللاتيني"كمْ" "how much" وتعكس حقيقة احتواء النماذج الكمومية دائماً على شيء ما في كميات منفصلة. الطاقة الكامنة في حقل كمومي تأتي بشكل مضاعفات صحيحة لبعض الطاقة الأساسية، بالنسبة للضوء يترافق ذلك مع تردد وطول موجة الضوء، الضوء قصير طول الموجة وعالي التردد له طاقة مميزة كبيرة. بينما يكون للضوء ذي طول الموجة الكبير والتردد القليل طاقة مميزة صغيرة.
في كلا الحالتين، مع ذلك، الطاقة الكلية الكامنة في حقل ضوئي خاص هي مضاعفات صحيحة لتلك الطاقة -1-2-14-137 ضعفاً- وليست أبداً عدداً كسرياً كـ 1.5 أو ᴨ أو الجذر التربيعي لـ 2. يمكن رؤية هذه الخاصية أيضاً على مستويات الطاقة المنفصلة للذرات، وطاقة الترابط في الأجسام الصلبة- يسمح بقيم محددة للطاقة، ولا يمكن أن يسمح بغيرها.
تعمل الساعة الذرية بسبب عدم الترابط في ميكانيكا الكمّ، باستخدام تردد الضوء المرتبط بحالتين انتقاليتين محددتين في السيزيوم لحفظ الوقت عند المستوى المطلوب حيث كانت الثانية الكبيسة leap second من المواضيع الأكثر نقاشاً الاسبوع الماضي.
ويمكن استخدام التحليل الطيفي فائق الدقة للبحث عن أشياء كالمادة المظلمة وهي جزء من أهداف لمعهد الفيزياء الأساسية منخفضة الطاقة low-energy fundamental physics institute.. ليس من الواضح دوما - حتى بالنسبة لبعض المواد الكمومية أساساً، كالطاقة الإشعاعية للجسم الأسود black-body radiation، إذ تظهر وكأنها تتضمن توزيعات مستمرة، ولكن هناك دائماً نوع من التقسيم للواقع القائم إذا قمت بالبحث في الرياضيات، وهذا جزء كبير مما يؤدي إلى الغرابة في النظرية.
الجسم الأسود هو الجسم الذي يمكنه امتصاص كل الأشعة التي تقع عليه، ليبقى في حالة توازن حراري، وعليه أن يصدر نفس المقدار من الأشعة التي يقوم بامتصاصها، وبالتالي فالجسم الأسود يشع بشكل جيد، الأفران مثال على ذلك.
- فيزياء الكم احتمالية
تعود ملكية الصورة لغراهام باركلي، بلومبيرغ نيوز
أحد أكثر الجوانب المفاجئة والمثيرة للجدل (تاريخياً على الأقل) في فيزياء الكم أنه من المستحيل التنبؤ بنتائج تجربة واحدة بشكل لا ريب فيه في نظام كمومي. لدى قيام الفيزيائيين بالتنبؤ بنتائج بعض التجارب، فإن التنبؤ يأخذ دوماً صيغة العثور على كل من النتائج المحتملة خصوصاً، وتتضمن المقارنات بين التجربة والنظرية دلائل تصنيفات احتمالية للعديد من التجارب المكررة.
عادة ما يأخذ الوصف الرياضي لنظام احتمالي صيغة دالة موجية wavefunction، يتم تمثيله عادة في المعادلات بالحرف اليوناني Psi ، هناك العديد من المناقشات حول ما تمثله بالضبط هذه الدالة الموجية، مؤدية إلى ظهور معسكرين أساسيين: أولائك الذين يفكرون بالدالة الموجية كشيء فيزيائي حقيقي، العبارة الاصطلاحية لذلك هي نظريات (أونتيك) ontic (وتعني النظرية الوجودية) ما دفع بعض الأشخاص ذوي الحس الفكاهي لتسمية مؤيديها بساي أونتولوجيست psi-ontologists) Ontology) (هي دراسة فلسفية تتناول الوجود والعلاقة بين مكوناته).
وأولئك الذين يفكرون بالدالة الموجية كتعبير فقط عن معرفتنا (أو عدمها) فيما يتعلق بالحالة الكامنة لجسم كمومي معين (نظريات المعرفة “epistemic ” theories) على أي مستوى من النماذج الأساسية، لا يُعطى احتمال إيجاد نتيجة على الفور باستخدام الدالة الموجية.
ولكن باستخدام مربع الدالة الموجية (كلام مفكك، أياً يكن، الدالة الموجية هي تكوين عقدي رياضياً (بمعنى أنه يتضمن أعداداً تخيلية كالجذر التربيعي لعدد سالب) وعملية الحصول على الاحتمالية أكثر أهمية بقليل، ولكن مربع الدالة الموجية كافٍ للحصول على الفكرة الأساسية. يدعى ذلك بـ ( قاعدة بورن“Born Rule”) بعد أن كان الفيزيائي الألماني ماكس بورن Max Born أول من اقترح ذلك،( في حاشية ورقة تعود للعام 1926 ) ويهاجم بعض الناس بأنهم إضافات خاصة بشعة.
هناك جهود فعالة في بعض الأجزاء من جماهير مؤسسات الكوانتم لإيجاد طريقة لاشتقاق قاعدة بورن من مبادئ أكثر أساسية؛ حتى تاريخه، لم تُصب أي منها نجاحاً تاماً، لكنها تخلق المزيد من العلوم المثيرة للاهتمام.
هذا الجزء من النظرية يقود أيضا إلى الأشياء التي تشبه الجزيئات متعددة الحالات في الوقت نفسه. كل ما يمكن التنبؤ به هو احتمالي، وقبل القياس الذي يحدد نتيجة معينة يكون النظام الذي يتم قياسه في حالة غير معروفة تعين رياضياً لتطابق كل الاحتمالات مع احتمالات مختلفة، اعتبارك ذلك النظام موجود فعلياً في جميع الحالات بنفس الوقت، أو مجرد كونه في حالة غير معروفة يعتمد بشكل كبير على موقفك تجاه كل من النموذجين الأونتيكي (الوجودي) والإيستيميك (المعرفي)، على الرغم من ذلك فإنهما يخضعان لأحد هذين النموذجين.
- فيزياء الكم عديمة التموضع
تجربة التخاطر الكمومي حقوق الصورة: IQOQI/Vienna
آخر المساهمات التي قدمها آينشتاين للفيزياء لم تُعرف على نطاق واسع على هذا النحو، على الأغلب يعود ذلك لأنه كان مخطئاً. في العام 1935 قدم أينشتاين في ورقة مع زملائه الأحدث بوريس بودولسكي Boris Podolsky) وناثان روزن Nathan Rosen (EPR ورقة “EPR paper”) وهي عبارة رياضية واضحة لشيء أثار قلقه بعض الوقت، فكرة ندعوها الآن (الترابط).
زعمت ورقة EPR أن فيزياء الكم التي تسمح بوجود أنظمة يتم فيها إجراء القياسات على مدى مواقع منفصلة للغاية يمكن أن تكون مترابطة للغاية، ويشار فيها إلى النتائج كنتائج محددة الواحدة تلو الأخرى. زعموا أن ذلك سيعني أن القياسات الناتجة تُحدد سلفاً، عبر عامل مشترك، لأن البديل سيتطلب نقل نتيجة أحد القياسات إلى موقع آخر للقياس (هدف آخر يتم قياسه) بسرعة أكبر من سرعة الضوء.
وبالتالي على ميكانيكا الكمّ أن يكون غير مكتمل، مجرد تقريب لنظرية أعمق بعض الشيء، (نظرية المتغيرات الموضعية الخفية، حيث لا تعتمد نتائج القياس التي يتم إجراؤها على أي شيء "بعيداً عن موقع القياس" على أكثر من إشارة تنتقل بسرعة الضوء (موضعية)، ولكن يتم تحديدها عبر عوامل مشتركة في كلا النظامين في الأزواج المتشابكة (المتغيرات الخفية).
اعتُبر ذلك حاشية غريبة لأكثر من ثلاثين سنة، إذ بدا وكأنه لا توجد طريقة لاختبار ذلك، ولكن في منتصف ستينيات القرن الماضي قام الفيزيائي الأيرلندي جون بيل John Bell بالتحقيق في ورقة EPR بمزيد من التفصيل. أظهر بيل أنه بإمكانك إيجاد ظروف يمكن بها لميكانيكا الكم التنبؤ بوجود روابط بين القياسات المتباعدة تكون أقوى من أي نظرية محتملة للنمط الذي أشار إليه كل من أينشتاين وروزن، وبودولسكي.
واختُبر ذلك تجريبياً في منتصف سبعينيات القرن الماضي على يد جون كلستر John Clauser، واعتبرت سلسلة من التجارب التي قام بها ألين أسبيكت Alain Aspect في أوائل ثمانينيات القرن الماضي بأنها أظهرت وبشكل واضح أنه لا يمكن شرح هذه الأنظمة المترابطة بأي نظرية تشير إلى المتغيرات الخفية على نطاق واسع.
المنهج الأكثر شيوعاً لفهم هذه النتيجة هو القول بعدم تموضع الميكانيك الكمي: حيث أن نتائج القياسات التي تُجرى في مواضع معينة تعتمد بطريقة ما على خصائص أجسام بعيدة حيث لا يمكن شرح ذلك باستخدام إشارات تنتقل بسرعة الضوء، مع ذلك، فإنه من غير المسموح إرسال معلومات بسرعة تتجاوز سرعة الضوء، بالرغم من وجود عدد من المحاولات لإيجاد طريقة لفعل ذلك باستخدام عدم التموضع الكمومي.
دحض ذلك تحولٌ إلى مشروع منتج بطريقة مثيرة للاستغراب- لمزيد من التفاصيل تحقق من مقال ديفيد كايسر David Kaiser (كيف حفظ الهيبيون الفيزياء How the Hippies Saved Physics)- عدم تموضع الكم هو أيضاً مشكلة محورية في المعلومات عن تبخر الثقوب السوداء، والجدل حول جدار الحماية firewall الذي خلق الكثير من النشاط مؤخراً. هناك أيضاً الكثير من الأفكار الجذرية بما فيها الصلة الرياضية للجسيمات المتشابكة التي وصفت في ورقة ERP والثقوب الدودية wormholes.
- فيزياء الكم غالباً ما تكون صغيرة جداً
ذرة الهيدروجين كما تبدو من تلسكوب كمومي حقوق الصورة: Stodolna et al. Phys. Rev. Lett.
تملك فيزياء الكم السمعة بكونها غريبة لأن تنبؤاتها لا تشبه بشكل كبير تجاربنا اليومية (على الأقل – الخيال الموجود في كتابي لا يبدو غريباً حتى بالنسبة للكلاب). يحدث ذلك لأن التأثيرات التي يتضمنها تغدو أصغر كلما أصبحت الأجسام أكبر. إذا أردت رؤية سلوك كمومي لا لبس فيه، فأنت بالأساس تريد رؤية الجسيمات وهي تسلك سلوك الموجات ويتناقص طول الموجة بزيادة الزخم.
الطول الموجي للأشياء المرئية مثل كلب يمشي عبر الغرفة صغير لدرجة مثيرة للسخرية فيما لو قمت بتمديد كل شيء بحيث تكون ذرة واحدة في هذه الغرفة بحجم النظام الشمسي بأكمله، طول موجة الكلب سيكون مماثلاً لحجم هذه الذرة نسبة إلى النظام الشمسي، هذا يعني أنه بالنسبة للجزء الأكبر، تقتصر الظاهرة الكمومية على مقياس الذرات والجزيئات الأساسية.
حيث تكون الكتل والسرعات صغيرة لدرجة كافية لتغدو الأطوال الموجية كبيرة بشكل كاف لتتم ملاحظتها بشكل مباشر. رغم ذلك هناك مجهود فعال في العديد من المجالات، لدفع حجوم الأنظمة التي تظهر التأثير الكمومي لتصل إلى حجوم أكبر. لقد قمت بتدوين الكثير حول مجموعة من التجارب التي قامت بها مجموعة ماركوس أرندلت Markus Arndt تظهر سلوكا شبيهاً بالسلوك الموجي على جزيئات أكبر فأكبر.
وهناك العديد من المجموعات في (ثغرة الميكانيك البصري cavity opto-mechanics) تحاول استخدام الضوء لإبطاء حركة قطع من السيليكون إلى النقطة التي ستصبح فيها الطبيعة الكمومية المنفصلة للحركة واضحة جداً. هناك العديد من الاقتراحات بأنه قد يمكن القيام بذلك باستخدام مرايا معلقة، لديها كتل من عدة غرامات، والتي ستكون ممتازة بشكل مثير للدهشة.
- فيزياء الكم ليست سحراً
صورة مأخوذة من " Surviving the World" للمؤلف: Dante Shepherd
النقطة السابقة تقود بشكل طبيعي إلى هذه: بالقدر الذي تبدو عليه من الغرابة، ففيزياء الكم بكل تأكيد ليست سحرية، الأشياء التي تقوم بالتنبؤ بها غريبة بمعايير الفيزياء اليومية، ولكنها مقيدة بصرامة بالمبادئ والقواعد الرياضية المفهومة جيداً.
إذاً، إذا جاء أحدهم إليك بفكرة كمومية بدا أنها من الجيد جداً أن تكون حقيقية- الطاقة الحرة، طاقات الشفاء الباطنية، رحلات الفضاء المستحيلة، فإنها غالباً ما تكون كذلك، هذا لا يعني بأننا لا نستطيع استخدام ميكانيكا الكم للقيام بأشياء مدهشة، تستطيع أن تجد البعض في (فيزياء جميلة فعلاً في التكنولوجيا الدنيوية really cool physics in mundane technology) ولكن هذه الأشياء تبقى ضمن حدود قوانين الديناميكا الحرارية والمنطق السليم.
الآن ها هي لديك :الضرورات الجوهرية لفيزياء الكم، من الممكن أن أكون قد أغفلت بعض النقاط، أو قمت بصياغة بعض العبارات التي ليست على درجة كبيرة من الدقة لترضي الجميع، ولكن هذا يجب أن يكون على الأقل بمثابة نقطة انطلاق مفيدة لمزيد من المناقشة.
