إن الظواهر التي تتضمن التوتر السطحي معقدة للغاية ولها تطبيقات في حياتنا اليومية، ويعالج الباحثون في معهد أوكيناوا للعلوم والتكنولوجيا (OIST) هذه الرياضيات المعقدة وراء الفيزياء الخاصة بتلك الظاهرة.
ونجد أن لآثار التوتر السطحي أهمية محورية في العديد من الظواهر اليومية: فهي الظاهرة التي تسبب التصاق قطرات صغيرة من المطر بنوافذك، وتكوّن فقاعات عند إضافة المنظفات إلى حوض مغسلتك، وتدفع الحشرات في مشيها على سطح الماء.
كما أنها تحرض تشكل دموع النبيذ (tears of wine) وهي حلقةٌ من سائلٍ شفاف بلقرب من أعلى الحافة الداخلية لكوب نبيذ والذي تتكون فيه القطرات بشكلٍ مستمر وتسقط مرة أخرى إلى النبيذ في الأسفل. لكن ورغم تواجدها الكلي والتاريخ الطويل من التأمل العلمي؛ إلا أن التوتر السطحي وتفاعل السوائل مع توترات سطحية مختلفة أمر غير مفهوم بالكامل بعد. ولعقود طويلة، استخدمت نماذج مبسطة لمواجهة تعقيد المشكلة.
أما الآن، فقد خطا الباحثون في (OIST) خطوةً جديدةً نحو فهمٍ أكثر اكتمالًا، من خلال معالجة خاصية معقدة من التوتر السطحي، وقد نُشر عملهم في مجلة ميكانيكا الموائع (Journal of Fluid Mechanics). وتكشف النتائج أن نهجًا تقريبيًا شائعًا في الاستخدام يعطي نتائج دقيقة مفاجئة رغم تعقيد المسألة.
هذا العمل هو استمرارٌ لدراساتٍ سابقة درس فيها علماء (OIST) حركة قطرات الأسيتون الناتجة عن التوتر السطحي، والتي تنزلق على سطح الماء.
يقول الدكتور ستوفيل جانسنس (Dr.Stoffel Janssens): "لأن الظاهرة معقدة للغاية؛ فكرت في أبسط نظام لم يُدرس بعد، محاولًا توقع القوى المؤثرة على القطرات مسببةً حركتها، وهذه خطوة صغيرة نحو فهم كامل لكيفية تحرك قطرةٍ من سائل على الماء بسبب التوتر السطحي".
وقد صمّم الباحثون في وحدة الرياضيات والميكانيكا والمواد برئاسة البروفيسور إليوت فريد (Eliot Fried) جهازًا بسيطًا على شكل وعاء مستطيل مليء بالماء تُغمر فيه أسطوانة ثابتة بالماء جزئيًا.
ويُضاف عامل خافض للتوتر السطحي (Surfactant) وهو جزيء عضوي يقلل التوتر السطحي على سطح الماء على أحد جانبي الأسطوانة، مما يسمح للعلماء بقياس خصائص الأجزاء الخالية من العامل السطحي والأجزاء المضاف لها عامل خفض التوتر السطحي (العامل السطحي). وقد ساعدت هذه القياسات العلماء على بناء نموذجٍ نظري يستخدم لتحديد القوى الفاعلة في الأسطوانة.
ويكمن جوهر التعقيد في الهندسة: إذ يميل سطح الماء نحو الأسطوانة ويعتمد الميل مباشرة على التوتر السطحي، وبوجود العامل المخفض للتوتر السطحي في أحد جانبي الأسطوانة تصبح خصائص سطح الماء على جانبي الأسطوانة غير متماثلة بسبب الانحناءات المختلفة، مما يجعل حساب القوى على الأسطوانة أكثر تعقيدًا من الناحية الرياضية. وقد تجاهل نموذج مبسط هذه الانحناءات _حتى الآن_ بدعوى افتراض أنّ سطح الماء لا يزال مستويًا تمامًا على جانبي الأسطوانة.
وقد وصف العلماء هذه المشكلة بثلاث مقاربات مستقلة: فقاموا أولًا بحساب القوى الميكانيكية المطبقة على الأسطوانة عدديًا، كما حصلوا على حلول حاسوبية للمعادلات المعقدة, ثم انتقلوا من النتائج الرقمية إلى الطريقة التحليلية، ويشار إليها أيضًا بأسلوب الورقة والقلم (pen and paper) للتحقق من النموذج.
ويقول البروفسور فريد: "في الطريقة العددية عليك إدخال الخوارزمية مع قيم الإدخال، يشبه الأمر بمعنى آخر حلك المعادلات لحالاتٍ نوعيةٍ جدًا، فيمكنك الشعور بما يجري ولكن لا يمكنك تقديم برهانٍ عام، وإن كنت تفعل ذلك تحليليًا باستخدام الورقة والقلم دون اختيار قيم عددية معينة، حينها يصبح لديك ما يمكن تعميمه".
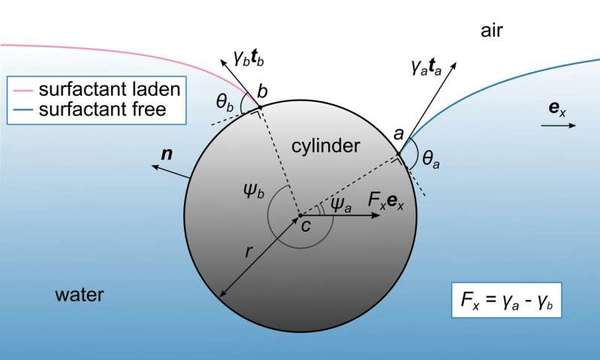
وأخيرًا، قام الباحثون بتحليل المشكلة باستخدام نهج مستقل ثالث يقوم على الطاقة بدلًا من القوى الميكانيكية. وأدت الطرق الثلاث إلى النتيجة ذاتها وغير المتوقعة: يمكننا تجاهل الانحناءات الحاصلة من تماس سطح الماء- الهواء لأن القوى المحسوبة تساوي تلك التي حصلنا عليها باستخدام النموذج المبسط، والذي يفترض أن سطح الماء مستوٍ.
وقال الدكتور جانسنس: "لا يمكننا استبعاد احتمال أن إهمال انحناء سطح ماء- هواء سيؤدي إلى أخطاء غير مقبولة، ومع ذلك، من المثير للدهشة اكتشافنا أن النموذج المبسط المستخدم لعقود دقيقٌ للغاية!" .
وما يتفوق على حل مشكلةٍ معقدة هو الثقة التي زودتنا بها نتائج هذا البحث بقياسات مثل توازن لانغموير (Langmuir) التي استُخدمت طوال القرن الماضي. بالإضافة إلى أنها الخطوة الأولى نحو فهم الظاهرة المعقدة لانزلاق قطرة الأسيتون على الماء بسبب التوتر السطحي.
ويختتم البروفسور فريد قائلا: "يمكن النظر إلى هذا العمل على أنه مقاربةٌ مختزلة، حيث عدنا خطوةً إلى الوراء في دراسة هذه الظاهرة المعقدة للغاية محاولين حلها بدءًا من السمات الأساسية. والآن يمكننا الانتقال إلى مشكلة أكثر تحديًا إلى حد ما، من قبيل المكان الذي سيُسمح فيه للأسطوانة أن تنزلق على سطح السائل".

