برهن الفيزيائيون تجريبياً على طريقة كمية بحتة لحل نظم المعادلات الخطية، إذ لهذه الطريقة القدرة على العمل بشكلٍ أسرع بأضعاف مضاعفة من أفضل الأساليب الكلاسيكية، وتظهر النتائج أن الحوسبة الكمومية قد يكون لها في نهاية المطاف تطبيقات عملية بعيدة المدى، وذلك لأن حل النظم الخطية أمر شائع في العلوم والهندسة.
عمل الفيزيائيون بقيادة هاوهوا وانغ Haohua Wang في جامعة تشجيانغ وتشاو يانغ لو Chao-Yang Lu وشياو بو تشو Xiaobo Zhu في جامعة العلوم والتكنولوجيا الصينية -جنباً إلى جنب مع باحثين مشاركين من مختلف المؤسسات في الصين- وقد نُشرت هذه الورقة البحثية كما أشاروا لها تحت عنوان "حلّال الكموميات الخطية"، في مقال صدر مؤخراً في مجلة Physical Review Letters.
وصرح لو لموقع phys.org: "برهنا للمرة الأولى عن خوارزمية كمية لحل أنظمة المعادلات الخطية على دارة كمية فائقة التوصيل، وهي واحدة من أفضل منصات الحالة الصلبة (تستخدم الخواص الإلكترونية لأنصاف النواقل) مع تدرجية ممتازة ودقة عالية ملحوظة".
وتسمى الخوارزمية الكمومية التي نفذوها خوارزمية هارو، هاسيديم، لويد (HHL Harrow, Hassidim, and Lloyd)، وكانت سابقاً تبدي القدرة -من حيث المبدأ- على أن تؤدي إلى تسريع كمومي أسي على الخوارزميات الكلاسيكية. ومع ذلك، لم يُثبت ذلك تجريبياً حتى الآن.
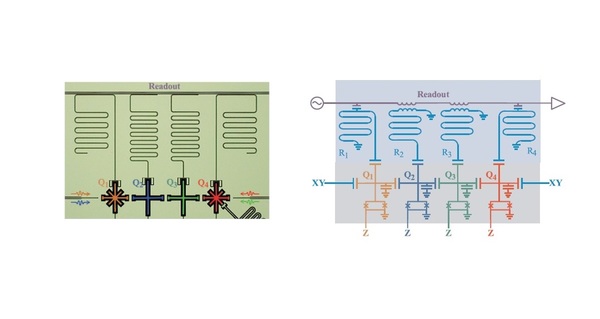
وبين العلماء في الدراسة الجديدة، أن الدارة الكمومية فائقة التوصيل التي تشغّل خوارزمية HHL، يمكن أن تحل أبسط نوع من النظام الخطي المتضمن معادلتين بمتغيرين. وتستخدم الطريقة أربعة كيوبتات qubits، أي بت مساعد واحد فقط (مكون عالمي لمعظم نظم الحوسبة الكمومية) وثلاثة كيوبيتات تقابل متجه الإدخال (b) والحلان المتمثلان في متجه الحل x في النظام الخطي القياسي Ax = b، حيث A هو مصفوفة مربعة \(2×2\).
ومن خلال إنجاز سلاسل من التناوب وعمليات التبادل بين الحالات والتحويلات الثنائية، تحدد خوارزمية HHL الحلول لهذا النظام، التي يمكن قراءتها بعد ذلك عبر قياس عدم الهدم الكمي quantum nondemolition measurement QND (أكثر طرق القياس الكمية كلاسيكيةً وفيها يكون التأثير على المنظومة المدروسة حين القياس بحدوده الدنيا)، ووضح الباحثون الطريقة باستخدام 18 متجه إدخال مختلف والمصفوفة نفسها، فنتجت حلول مختلفة للمدخلات المختلفة.
ويشير الباحثون، أنه من السابق لأوانه القول كم ستكون هذه الطريقة الكمومية أسرع في العمل طالما أن هذه المسائل تُحل بسهولة بالطرق الكلاسيكية.
وقال تشو: "تستغرق العملية الحسابية بأكملها ما يقارب الثانية الواحدة، ومن الصعب الآن إجراء مقارنة مباشرة ما بين الإصدار الحالي والأساليب الكلاسيكية، ففي هذا العمل، بيّنّا كيفية حل أبسط الأنظمة الخطية ذات المصفوفات المربعة \(2×2\)، الممكن حلها بالطرق الكلاسيكية في وقتٍ قصيرٍ جداً. وتكمن القدرة الأساسية للخوارزمية الكمومية HHL في أنها عند حل مصفوفة نظام متفرق "s-sparse"system matrix من حجم كبير جداً، يمكن الحصول على تسارع أسي مقارنةً مع أفضل طريقة كلاسيكية. لذلك، سيكون أمراً أكثر أهمية إظهار هذه المقارنة عندما تقفز المعادلة الخطية لتصبح نظاماً كبيراً جداً."
ويتوقع الباحثون في المستقبل أن بالإمكان توسيع نطاق هذه الدارة الكمومية لحل أنظمة خطية أكبر، كما يخططون لتحسين أداء النظام بشكل أكبر عبر إجراء بعض التعديلات المباشرة على تصنيع الجهاز لتقليل بعض الأخطاء في تنفيذه. وبالإضافة إلى ذلك، يريد الباحثون تحري الكيفية التي يمكن استخدام الدارة بها لتنفيذ خوارزميات كمومية أخرى لمجموعة متنوعة من التطبيقات واسعة النطاق.
ويضيف وانغ: "إن بحثنا المستقبلي سيركز على تحسين أداء المعدات، بما في ذلك أزمنة ترابط منطقي أطول وبوابات منطقية عالية الدقة، وعدد أكبر من الكيوبتات وتداخل أقل وتحسين دقة القراءة، وما إلى ذلك. واستناداً إلى تطور الأجهزة، سنبرهن على المزيد من الخوارزميات الكمومية ونحسنها لنبين حقيقة قدرة معالج الكم فائق التوصيل."

