يُعتبر الرقم 6174 رقمًا غامضًا بجدارة، وذلك لايبدو واضحًا من الوهلة الأولى، لكن وبمجرد أن نرى ما نحن على وشك أن نراه، ولأي شخصٍ يستطيع الطرح، فإمكانه حل الغموض الذي يجعل من العدد 6174 مميزاً جداً.
عملية كابريكار:
في عام ١٩٤٩ قام عالم الرياضيات كابريكار D. R. Kaprekar من ديفلالي-الهند بتصميم عملية تعرف الآن باسم عملية كابريكار.
اختر أولاً عدداً مؤلفاً من أربع منازل مختلفة (أي ليست من الشكل 1111 أو 2222 إلخ...)، ثم أعد ترتيب الأرقام للحصول على أكبر وأصغر عدد يمكن أن تشكّله هذه الأرقام، وأخيراً اطرح أصغر عدد من أكبر عدد للحصول على عدد جديد، ثم أعد العملية لكل عدد جديد ناتج.
إنها عملية بسيطة، لكن اكتشاف عالم الرياضيات كابريكار قاد إلى نتائج مفاجئة. لنستوعب ما حصل دعنا نحاول مع العدد 2005، وهو يمثل إحدى السنوات الماضية، أكبر عدد يمكن تشكيله من أرقام العدد 2005 هو العدد 5200، وأصغر عدد يمكن تشكيله هو 0025، أو 25 (إن كان أحد الأرقام أو أكثر مساوٍ للصفر، فإننا نضعه على يسار أصغر عدد)، عملية الطرح هي:
\(5200 - 0025 = 5175 \)
\(7551 - 1557 = 5994 \)
\(9954 - 4599 = 5355 \)
\(5553 - 3555 = 1998 \)
\(9981 - 1899 = 8082 \)
\(8820 - 0288 = 8532 \)
\(8532 - 2358 = 6174 \)
\(7641 - 1467 = 6174 \)
عند الوصول إلى العدد 6174 فإن العملية تُكرر نفسها، معطيةً العدد 6174 في كل مرة، ندعو العدد 6174 لُب هذه العملية، لذلك فإن العدد 6174 هو جوهر عملية كابريكار، لكن هل هذا مميز بقدر ما يعطي 6174؟ حسنًا، ليس العدد 6174 هو العدد الجوهري الوحيد في هذه العملية، إنها تحمل مفاجآت جديدة في جعبتها، لنقم بتجربة عددٍ مختلف، وليكن مثلا 1789:
\(9871 - 1789 = 8082 \)
\(8820 - 0288 = 8532 \)
\(8532 - 2358 = 6174 \)
حصلنا على العدد 6174 مجدداً!
عندما بدأنا بالعدد 2005 وصلت العملية إلى العدد 6174 في سبع خطوات، وفي العدد 1789 في ثلاث خطوات. في الواقع، ستصل إلى العدد 6174 لكل عدد مؤلف من أربع منازل مختلفة. إنها مذهلة، أليس كذلك؟ عملية كابريكار بسيطة جداً لكنها تكشف النقاب عن نتيجة مميزة، وهذا سيصبح أكثر إثارة للاهتمام عند التفكير حول سبب أن كل الأعداد المؤلفة من أربع منازل تعطي العدد 6174 ضمن عملية كابريكار.
لماذا فقط 6174؟
الأرقام لأي عدد مؤلف من أربع منازل يمكن أن يعاد ترتيبها لتشكل أكبر عدد من خلال ترتيب العوامل بشكلٍ تنازلي، وتعطي أصغر عدد من خلال ترتيب العوامل بشكل تصاعدي، وذلك لأربعة أرقام تمثل a,b,c,d ، حيث:
\(9 ≥ a ≥ b ≥ c ≥ d ≥ 0 \)
و a, b, c, d ليست نفس الرقم، أكبر عدد هو abcd و أصغر عدد هو dcba.
يمكن حساب نتيجة عملية كابريكار باستخدام الطريقة المعيارية للطرح، والمطبقة في كل عمود من هذه المسألة:
a b c d
- d c b a
ــــــــــــــــ
A B C D
والذي يعطي العلاقات:
\(D = 10 + d - a (as a > d)\)
\(C = 10 + c - 1 - b = 9 + c - b (as b > c - 1) \)
\(B = b - 1 - c (as b > c) \)
\(A = a - d \)
لهذه الأرقام، حيث: a>b>c>d
سيُعاد تكرار العدد ضمن عملية كابريكار إذا كان العدد الناتج (ABCD) يمكن إعادة كتابته باستخدام الأرقام الابتدائية (a, b, c, d)، لذلك نستطيع إيجاد النواتج لعملية كابريكار من خلال الأخذ بعين الاعتبار كل الحالات الممكنة للأعداد المُشكّلة بالأرقام {a, b, c, d} ، والتأكد فيما إذا كانت تُحقق العلاقة التي في الأعلى.
( !4=24) تعطي جميع الحالات الممكنة لنظام من أربع معادلات متسلسلة ذات أربعة مجاهيل، لذلك يجب أن نكون قادرين على حل هذا النظام بالمتغيرات a, b, c, d.
تبيَّن أن واحدة فقط من هذه الحالات لها حل صحيح والذي يحقق (\(9 ≥ a ≥ b ≥ c ≥ d ≥ 0\) )، وتلك الحالة هي: ABCD = bdac
والحل لهذه المعدلات المتسلسلة هو:
a=7، b=6 ، c=4 ، d=1
والذي هو العدد ( ABCD = 6174 )، ولا يوجد أي حلول منطقية للمعادلات المتسلسلة الناتجة من بعض العوامل مثل {a,b,c,d} وتكون متساوية، بالتالي فإن العدد 6174 هو العدد الوحيد الغير مُتغير بالنسبة لعملية كابريكار ـ عددنا الغامض فريد من نوعه.
لكن ومن أجل العدد المؤلف من ثلاث منازل، تأتي نفس الظاهرة.على سيبل المثال بتطبيق عملية كابريكار على العدد 753 المؤلف من ثلاث منازل، يعطي:
\(753 - 357 = 396 \)
\(963 - 369 = 594 \)
\(954 - 459 = 495\)
\(954 - 459 = 495 \)
العدد 495 هو الناتج الفريد للعملية على العدد المؤلف من ثلاث منازل، وكل الأعداد المؤلفة من ثلاث منازل ستصل العدد 495 باستخدام العملية، جربها بنفسك وستعرف مدى صحتها.
ما هي سرعة الوصول الى 6174؟
يقول كاتب هذا المقال: عندما سمعت لأول مرة بالعدد 6174 في عام 1975 من صديق، كنت متأثراً للغاية في ذلك الوقت، كنت أعتقد أن إثبات هذه الظاهرة أمرٌ سهل، لكني لم أعرف السبب الحقيقي وراء ذلك. استخدمت الحاسوب للتحقق فيما إذا كانت كل الأعداد ذات الأربعة عوامل ستصل إلى العدد الجوهري 6174، في عدد محدود من الخطوات. البرنامج الذي استخدمته كان بحوالي 50 جملة منطقية في برنامج Visual Basic، بحيث تحقق من كل الأعداد من 1000الى 9999 والتي لا تتشابه أرقام خاناتها.
الجدول في الأسفل يوضح النتائج، كل عدد مؤلف من أربعة منازل، حيث الخانات غير متساوية، جميعها تصل إلى العدد ٦١٧٤ بتطبيق عملية كابريكار. وفي سبع خطوات على الأكثر، إذا لم تصل إلى العدد ٦١٧٤ بعد استخدام عملية كابريكار سبع مرات، عندها سيكون لديك خطأ حسابي ويجب عليك المحاولة مجدداً.
| Iteration | Frequency |
|---|---|
| 0 | 1 |
| 1 | 356 |
| 2 | 519 |
| 3 | 2124 |
| 4 | 1124 |
| 5 | 1379 |
| 6 | 1508 |
| 7 | 1980 |
أي الطرق تؤدي الى 6174 ؟
تحقق حاسوبي من كل الـ 8991 رقماً (وهي الأرقام المحصورة بين العددين 1000 و9999 وينطبق عليها شرط عدم تماثل جميع خاناتها)، لكن مالكوم لينز Malcolm Lines يوضح في مقالته أنَّ ذلك كافٍ للتحقق 30 حالة فقط من الحالات التي يمكن أن تشكلها الأعداد ذات الأربع منازل عند التحقق بعملية كابريكار.
وكما رأينا سابقاً لنفترض أنَّ العدد المؤلف من أربع منازل هو abcd ، حيث أنَّ:
\(9 ≥ a ≥ b ≥ c ≥ d ≥ 0 \)
لنقم بحساب عمليات الطرح الأربع الأولى في العملية.
العدد الأكبر هو 1000a+100b+10c+d والعدد الأصغر هو 1000d+100c+10b+a ، لذلك فإن عمليات الطرح هي:
\(1000a + 100b + 10c + d - (1000d + 100c + 10b + a) \)
\(= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a) \)
\(= 999(a-d) + 90(b-c) \)
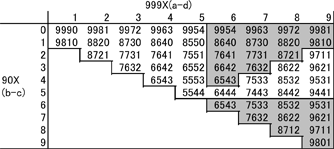
القيمة الممكنة لـ (a-d) تقع ما بين 1 و 9، والقيمة الممكنة لـ (b-c) تقع ما بين 0 و 9 . ومن خلال التجريب ضمن كل الحالات الممكنة، نستطيع رؤية كل النتائج الممكنة من عملية الطرح الأولى في العملية، هذا مبين في الجدول1.
نحن نهتم بالأعداد التي أرقامها ليست جميعها متشابهة، وحيث أن:
a ≥ b ≥ c ≥ d
لذلك نحن نحتاج فقط إلى اعتبار أن (a-d) ≥ (b-c)، لذلك نستيطع تجاهل المنطقة الرمادية في الجدول 1 والذي يحوي هذه الأعداد، أي:
(a-d) < (b-c)
الآن، نعيد ترتيب أرقام الأعداد في الجدول ضمن ترتيب تنازلي، للحصول على العدد الأكبر:
نسطتيع تجاهل التكرارات في الجدول 2 (المناطق الرمادية)، ويتبقى فقط 30 عدد للمتابعة بما تبقى من العملية. الشكل التالي يوضح المرات، والتي ستوصل إلى العدد 6174.
من هذا الشكل نستطيع رؤية كيف أن كل الأعداد ذات الأربعة أرقام ستصل إلى العدد 6174، وستصل إليه بسبع خطوات على الأكثر، وبالرغم من كل ذلك فما زلت أعتقد أنَّ هذا العدد غامضٌ جداً، وأعتقد أن كابريكار، وهو العالم الذي اكتشف هذا العدد، كان ذكياً جداً، أو أنه كان يمتلك الكثير من الوقت للتفكير بهذا العدد!
ماذا عن الأعداد ذات المنزلتين، أو الخمس منازل، أو الست ......؟
رأينا كيف أن الأعداد ذات الثلاث منازل و الأربع منازل تصل إلى جوهر فريد، لكن ماذا عن باقي الأعداد؟ تبَّين لاحقًا أنَّ الإجابة لتلك الأعداد ليست مذهلة، لنقم بالتحقق من عدد ذو منزلتين، وليكن 28:
\(82 - 28 = 54 \)
\(54 - 45 = 9 \)
\(90 - 09 = 81 \)
\(81 - 18 = 63 \)
\(63 - 36 = 27 \)
\(72 - 27 = 45 \)
\(54 - 45 = 9 \)
ربما لن يأخذ منك الأمر كثيراً للتحقق من أن كل الأعداد ذات المنزلتين، وعلى خلاف الأعداد ذات الأربع منازل، لن تصل إلى أي عددٍ جوهري، بالتالي لايوجد أي عدد جوهري فريد من أجل الأعداد ذات المنزلتين.
لكن ماذا عن الأعداد ذات الخمس منازل؟ هل هناك عدد جوهري يشابه العدد 6174 و 495؟ للإجابة عن هذا السؤال نحن نحتاج إلى استعمال عملية مشابهة كما السابق، والتحقق من 120 تركيبة محتملة للعوامل {a,b,c,d,e} من أجل ABCDE والذي يحقق:
\(9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0 \)
بحيث:
abcde - edcba = ABCDE
لحسن الحظ تم الحساب بواسطة الحاسوب، وصار معروفاً الآن أنه لايوجد أي عددٍ جوهري لعملية كابريكار على الأعداد المؤلفة من خمس منازل، لكن كل الأعداد ذات الخمس منازل ستصل إلى إحدى النواتج في الحلقات الثلاث التالية:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
وكما أشار مالكوم من مقالته، استغرق الأمر وقتاً طويلاً للتحقق مما حصل من أجل الأعداد ذات الست منازل أو أكثر، وعمله صار مملاً للغاية! ولحمايتك من هذا المصير فإن الجدول التالي يبين الأعداد الجوهرية من المرتبة الثانية إلى المرتبة العاشرة، وتبين أن عملية كابريكار تأخذ كل الأعداد إلى عدد جوهري فقط في حالة الأعداد ذات الأربع أو الثلاث منازل.
| Digits | Kernel |
|---|---|
| 2 | None |
| 3 | 495 |
| 4 | 6174 |
| 5 | None |
| 6 | 549945, 631764 |
| 7 | None |
| 8 | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| 10 | 6333176664, 9753086421, 9975084201 |
رائع، لكن هل هو مميز؟
رأينا كيف أن كل الأعداد ذات الثلاث منازل تصل إلى العدد 495، وأن كل الأعداد ذات الأربع منازل تصل إلى العدد 6174، وذلك باستخدام عملية كابريكار. لكنني لم أوضح لماذا كل تلك الأعداد تصل إلى عدد جوهري، هل هذه الظاهرة عرضية؟ أم أنه يوجد سبب رياضي عميق لحصول هذا؟ إنه رائع وغامض كما نتج، وربما يكون فقط صدفة.
ولنقف ونتأمل لغز جميل افترضه يوكيو ياماموتو Yukio Yamamoto من اليابان.
إذا ضربت عددين من خمس منازل وحصلت على الناتج 123456789، فهل بإمكانك معرفة العددين؟
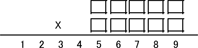
هذا لغز رائع جداً، وربما تعتقد أنه يوجد نظرية رياضية كبيرة تقف ورائه، لكن الواقع أنه جميل ولكنه فقط صدفة، وهناك أمثلة مشابهة جداً لكنها ليست بذات الروعة.
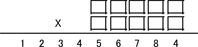
إذا أريتكم لغز Yamamoto سيكون مصدراً ملهماً لحله لأنه ببساطة جميل، لكن إن أريتكم اللغز الثاني ربما لن تعودوا مهتمين أبداً، أعتقد أنَّ مسألة كابريكار تشابه لغز عدد ياماموتو، أشرنا إلى اللغزين لأنهما رائعان جداً. ولأنهما كذلك، نشعر بأن هناك شيئاً مهماً بالنسبة لهما، في الوقت الذي ربما يكون جمالهما عرضيًّا، يوجد الكثير من سوء الفهم الذي قاد إلى تطورات في الرياضيات والعلوم في الماضي.
هل من الكافي معرفة أنَّ كل الأعداد ذات الأربع منازل تصل إلى العدد 6174 باستخدام عملية كابريكار، لكن دون معرفة السبب؟ حتى الآن، لا يوجد أي شخص قادر على القول أن كل الأعداد تصل إلى عدد جوهري هو ظاهرة عرضية متعلقة بالأعداد ذات الثلاث منازل والأربع منازل، تبدو هذه الخاصية مفاجئة جداً وتقودنا إلى افتراض أنَّ نظريات رياضية كبيرة تقف خلفها، وإذا أمكننا الإجابة عن هذا السؤال، ربما يمكننا فقط القول بأنه سوء فهم بسيط ورائع، لكننا نأمل أنه ليس كذلك.