معادلة أويلر
متطابقة أويلر هي مساواة وُجدت في الرياضيات، والتي تُقارن مع السوناتا الشيكيسبيرية، ووُصفت "بالمعادلة الأجمل على الإطلاق". وهي حالة خاصة من معادلة رئيسية في علم الحسابات المركبة تُدعى "صيغة أويلر"، التي وصفها الفيزيائي الكبير ريتشارد فاينمان Richard Feynman في محاضراته بأنها "جوهرتنا" و "الصيغة الأكثر شهرة في الرياضيات".
في مقابلةٍ مع قناة BBC، قال البرفيسور دايفيد بيرسي David Percy من معهد الرياضيات وتطبيقاتها، بأن متطابقة أويلر كانت "شيئاً تقليدياً حقيقياً ولا يمكنك ابتكار أفضل منها.. إنها بسيطة لتنظر إليها ولكنها تحمل أفكاراً عميقةً للغاية، وتتكون من الثوابت الخمسة الأكثر أهميةً في الرياضيات".
تُكتب متطابقة أويلر بالشكل البسيط:
\(e^{i \pi} +1=0 \)
الثوابت الخمسة هي
- العدد صفر 0.
- العدد واحد 1.
- العدد باي، عدد غير نسبي (مع أرقامه اللانهائية) والذي يساوي نسبة محيط الدائرة على قطر الدائرة. وتقارب قيمته 3.14159 …
- العدد e، وهو أيضاً عدد غير نسبي، وهو أساس اللوغارتم الطبيعي والذي ظهر بشكلٍ طبيعيٍّ من خلال دراسة الربح المركب والحساب، العدد e يعم الرياضيات، ويظهر على ما يبدو من اللاشيء في أعدادٍ كبيرةٍ من المعادلات ذات الأهمية. تُقارب قيمته 2.71828 ….
- العدد i، ويُعرف بأنه الجذر المربع للعدد (-1)، العدد الأكثر أهميةً بالنسبة للأعداد التخيلية، وسمي كذلك لأنه بالحقيقة لا يوجد أي عددٍ يمكن ضربه بنفسه ليكون الناتج عدداً بإشارةٍ سالبة (بالتالي الأعداد السالبة لا تملك جذوراً مربعةً حقيقية).
لكن في الرياضيات يوجد العديد من المواقف التي يجبر فيها المرء على أخذ الجذر التربيعي لعددٍ بإشارةٍ سالبة، فلذلك يوضع العدد i لتوضيح الأماكن التي حدث فيها ذلك.
رياضي مُنتج!
ولد الرياضي ليونارد أويلر Leonhard Euler في سويسرا في القرن الثامن عشر، والذي طور العديد من المفاهيم التي تعتبر جزءاً لا يتجزأ من الرياضيات الحديثة.
أمضى معظم مسيرته في جامعة سان بترسبرغ في روسيا، كان من أكثر الرياضيين غزارةً في التأليف في التاريخ، وبحسب الأكاديمية البحرية الأمريكية USNA، نُشر 886 كتاباً وورقةً بحثية. معظم مؤلفاته كانت في آخر عقدين من حياته، عندما كان أعمى بالكامل، كان هناك الكثير من الأعمال حيث أن أكاديمية سان بترسبرغ استمرت بنشر أعماله بعد وفاته لمدة ثلاثين عاماً!
تضمنت مساهمات أويلر "صيغة أويلر" و "نظرية أويلر"، وكلاهما تعني أشياء مختلفةً باختلاف المحتوى، وبحسب USNA في الميكانيكا توجد "زوايا أويلر (لتعيين اتجاه جسمٍ ثابت)، نظرية أويلر (كل دوران يملك محوراً)، معادلات أويلر لحركة السوائل، ومعادلة أويلر-لاغرانج (والتي أتت من حساب المتحولات)".
ضرب الأعداد المركبة
تنبع متطابقة أويلر بشكلٍ طبيعيٍّ من تفاعل الأعداد المركبة، والتي هي أعداد مؤلفة من جزئين: عدد حقيقي وعدد تخيلي، على سبيل المثال 4+3i. تظهر الأعداد المركبة في الكثير من التطبيقات مثل ميكانيكا الموجات (التابعة لميكانيكا الكم)، وتصميم الدوائر التي تستخدم التيار المتردد (وهو أمر شائع في الهندسة الكهربائية).
بالإضافة إلى ذلك، تمتلك الأعداد المركبة (وشبيهتها الأعداد المركبة الفائقة) خاصيةً تسمح باستخدامها بشكلٍ عمليٍّ في دراسة التصميم على الحاسوب والروبوتات والملاحة وديناميكية الطيران والميكانيكيات المدارية -عملية ضربهم مع بعضهم البعض تسبب لهم الدوران- وهذه الخاصية تسمح لنا بفهم المفاهيم الكامنة وراء متطابقة أويلر.
في المثال أدناه، خمسة أعداد مركبة وُضعت على "المستوى المركب" ويشكلون معاً "شكل منزل". يشابه المستوى المركب الخط الحقيقي، ما عدا أنه ببُعدين، يمثل الاتجاه الأفقي الأعداد الحقيقية، بينما يمثل الاتجاه العمودي الأعداد التخيلية. كل عدد مركب "بشكل المنزل" يكون مضروباً بالعدد المركب 4+3i، ثم يعاد رسمه (السهم الأخضر).
وكما نلاحظ، الضرب بالعدد المركب 4+3i ينتج عنه تمدد شكل المنزل (ازدياد مساحته وتحركه بعيداً عن النقطة الأصلية 0+0i بنفس الكمية) ودورانه (يميل بزاوية معينة)، ولإظهار هذا التأثير الخاص للضرب بالعدد 4+3i، ينتج نفس التأثير من خلال تكبير شكل المنزل خمس مرات وتدويره بزاوية 36.9 درجة (السهم الأحمر).
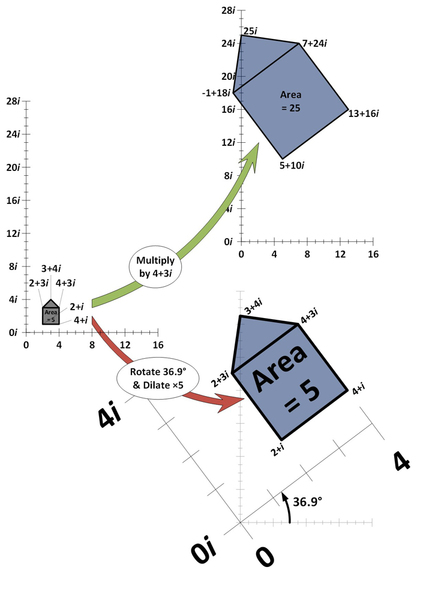
كميات مختلفة من التمدد والدوران يمكن أن تنتج تأثير الضرب بأي عددٍ من المستوى المركب.
الصيغة القطبية للأعداد المركبة
تتحدد كمية التوسع (dilation) والدوران (rotation) للعدد المركب من خلال خواص جوهرية بالنسبة للعدد 4+3i، وكما نرى بالشكل أدناه، هو خمس واحدات من الأصل (r=5) ويشكل زاويةً بقياس 36.9 درجة مع المحور الأفقي (φ = 36.9°). استخدمت هذه القياسات في ما يدعى الصيغة القطبية للأعدد المركبة \(re^{iφ}\)، على خلاف الصيغة المستطيلة المعتادة (a+bi).
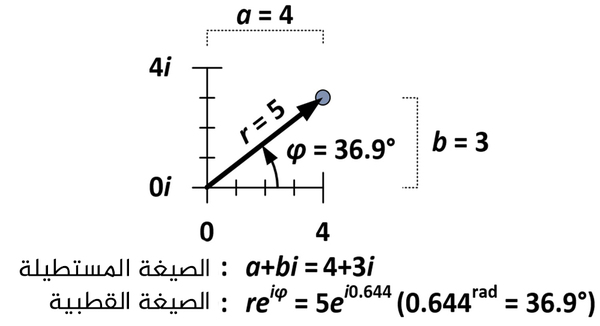
تتطلب الصيغة القطبية بأن يتم قياس الزاوية φ بالزاوية نصف القطرية "الراديان"، واحد راديان (1 rad) يساوي 57.3 درجة تقريباً، وهو قياس الزاوية التي تتشكل عندما يتم لف نصف قطر الدائرة حول محيط هذه الدائرة. ويساوي قياس باي راديان نصف طول محيط الدائرة، ويساوي قياس 2π راديان طول محيط الدائرة.
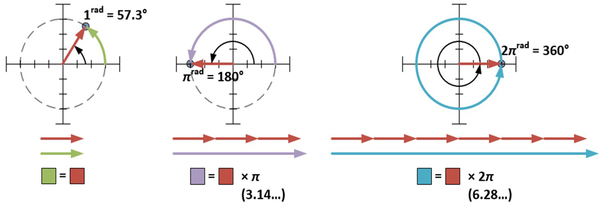
قياس الزاوية للعدد 4+3i هو 0.644، أي أن (36.9 درجة = 0.644 راديان) والذي يعني أن الصيغة القطبية للعدد 4+3i هي \(5e^{0.644}\). قياس r وφ يمكن أن يحدد أيضاً لكل النقاط المشكِّلة لشكل المنزل، طريقة أخرى لتحقق تأثير التمدد والدوران للضرب بالعدد 4+3i، هي بضرب كل r بالعدد 5، ثم أضف 36.9 درجة (أو 0.644 راديان) إلى كل φ.
ومن هذا الوصف نستطيع رؤية أنه عندما يتم ضرب الأعداد المركبة ببعضها البعض، فإنه يتم ضرب المسافات وجمع الزواية، وهذا يعزى إلى الخواص الجوهرية للأسس والتي يمكن رؤيتها جبرياً.
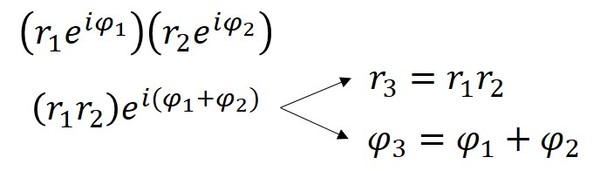
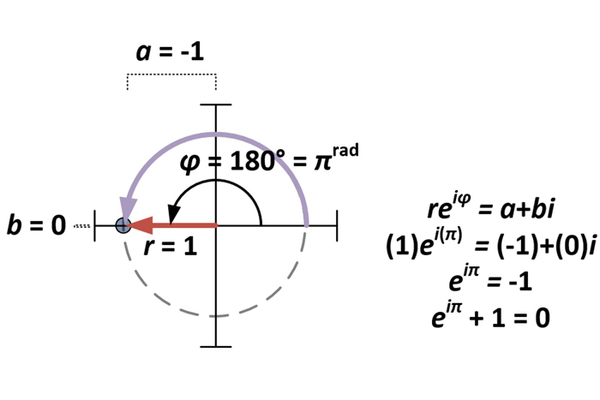
مع الصيغة القطبية للأعداد المركبة المعمول بها، فإن متطابقة أويلر هي حالة خاصة من a+bi حيث أن a=-1 وb=0، ونتيجة ذلك على الصيغة القطبية \(re^{iφ}\)، وهذا يؤدي إلى أن r=1 و φ=π (حيث أن π راديان= 180 درجة).
اشتقاق الصيغة القطبية
برغم أن متطابقة أويلر تنتج من الصيغة القطبية للأعداد المركبة، فإنه من المستحيل استخلاص الصيغة القطبية (وبالأخص عند الظهور الفجائي للعدد e) بدون حساب التفاضل والتكامل.
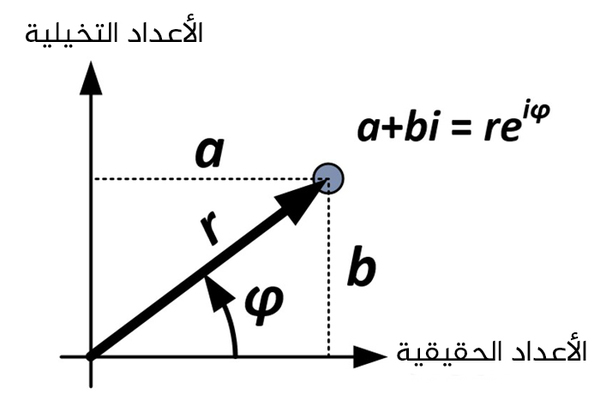
بدأنا بالصيغة المستطيلة للعدد المركب:
a + bi
من الشكل وحساب المثلثات، نستطيع كتابة البدائل الآتية:
\((r×cosφ)+(r×sinφ)i\)
نستطيع إخراج r كعامل مشترك:
\(r(cosφ+i sinφ)\)
عادة نسمي المقدار (\(cosφ+isinφ\)) بالرمز cisφ وهو اختصار "جيب التمام الموجب والجيب التخيلي" (Cosine plus Imaginary Sine).
اتضح أن الدالة cisφ مساوية للصيغة \(e^{iφ}\)، وهذا جزء يستحيل إظهاره بدون حساب التفاضل والتكامل.
كما هو معروض في الاشتقاقين أدناه:
لذلك، فإن الصيغة \(r cisφ \) تُكتب بالصيغة القطبية المعيارية بالشكل \( re^{iφ}\).


