هل يتغير انتشار حقل الجاذبية بشكلٍ لحظي؟ أم بسرعة الضوء؟ أو عند سرعاتٍ مختلفة؟
يقول داني نيفراث Danny Nevrath: "المشكلة الوحيدة مع سرعة الضوء هي أنّها تأتي في وقتٍ مبكرٍ جداً من الصباح". أحد أكثر الأسئلة التي تُطرح عليّ، هي فيما إذا كانت الجاذبية لحظيّة، أو فيما إذا كان هناك حدٌ لسرعة انتشار قوة الجاذبية. هذا ليس بالسؤال البسيط كما يبدو ظاهرياً.
في النهاية نحن نعرف سرعة حركة الضوء، وإذا ما اختفت الشمس فجأةً عن الوجود، سنستمر باستقبال الضوء القادم منها لمدة ثمان دقائق بعد اختفائها! لكن ماذا عن الجاذبية ومدار الأرض؟ هل ستُحلق الأرض ببساطةٍ على طول خطٍ مستقيمٍ مثل كرة "البوي" في اللحظة التي يتحطم بها الشريط؟
أم هل ستستمر في التحرك على مدارها الكوكبي لبعض الوقت، وقد تُعاني المزيد من التأثيرات المثيرة للاهتمام؟ صدّق أو لا تصدق، يعدّ هذا واحداً من أهم الاختلافات بين مدرسة نظريّة نيوتن القديمة ونظرية النسبية العامة لأينشتاين. فوفقاً لنيوتن، يكون لديك كتلتان تفصل بينهما مسافة، وتُحدّد القوة بذلك الأمر، إذا ما أخذت إحدى هاتين الكتلتين بعيداً وذهبت معهما القوة، ستنتهي القصة لحظياً.
لكن في النسبية العامة، تُصبح الأشياء أكثر تعقيداً، وهي مختلفةٌ جداً عن صورة نيوتن البسيطة التي ربما تعلمت عنها في المدرسة الثانوية أو الجامعة. في البداية، ليست الكتلة هي من يتسبب في الجاذبية؛ فكل أنواع الطاقة، -بما في ذلك الكتلة- تُؤثر على انحناء المكان. لذلك وبالنسبة للأرض والشمس، فإن الكتلة الكبيرة للشمس تُهيمن على انحناء المكان، وتتحرك الأرض على طول مدارٍ موجودٍ في المكان المنحني بشكلٍ مشابهٍ تماماً للأجسام الموجودة في النظام الشمسي.
في حال أزلت الشمس عبر التسبب بإخراجها من الوجود بطريقةٍ ما، ماذا سيحصل؟
في النسبية العامة، من الصحيح أن المكان سيعود ليصير مسطحاً، لكن ذلك ليس صحيحاً في كل نقطة. في الحقيقة وبشكلٍ مشابهٍ لتصرف سطح بركة ماءٍ عندما تُسقِط شيئاً ما فيها، فإنها ستعود مسطّحةً، ويصبح الاضطراب الحاصل على هيئة تموجاتٍ مرسلةٍ نحو الخارج!
في نظرية أينشتاين للجاذبية، تتحرك هذه التموجات بسرعة الضوء وليس بشكلٍ لحظي. يُرشدنا هذا الأمر إلى أنّ التشوه الحاصل في الزمكان بفعل المادة والطاقة -إضافةً إلى التغيرات الحاصلة في التشوه- يجب أن ينتشر بسرعة الضوء، وبالتالي لابد وأن تتساوى سرعتا الجاذبيّة والضوء في الخلاء.
هذه الفكرة مذهلة حقاً، وتقودني إلى طرح سؤالٍ آخر. فكّر بالأمر، لو كانت الأرض ساكنة، فإنها ستشعر بالتموجات في اتجاهٍ واحد، لكن لو كانت متحركةً فوق سطحٍ في الفضاء، هل ستشعر بالتموجات بشكلٍ مختلف؟
تبين أنه في الوقت الذي لم يكن فيه نيوتن مدركاً لسرعتك، عرف أينشتاين تلك السرعة. لن تمتلك الشمس -كما هي الآن- تأثيراً ثقالياً على الأرض لأكثر من 8 دقائق، والجاذبية التي تشعر بها الأرض الآن وكأنها تسحبها نحو الشمس، هي تقوم في الواقع بسحبها نحو المكان الذي كانت الشمس موجودةً فيه قبل ثمانِ دقائق. أليس ذلك غريباً؟
إن التغيرات الحاصلة في الجاذبية التي تُعاني منها الأرض، ناتجةٌ عن حقيقة أن مواضع وكمية حركة كل الأجسام في الكون -بما في ذلك الشمس- تتغير بمرور الزمن، ما يُغير من انحناء المكان في جوارنا.
لكن هل تودّ معرفة الشيء الذي يحتوي نوعاً من الالتباس؟ إذا ما كان ذلك هو الأمر الوحيد المختلف عن جاذبية نيوتن، ستكون نظرية أينشتاين خاطئة، حيث أن التنبؤات التي حصلنا عليها للمدارات الكوكبية والتي تعتمد على مكان وجود الشمس والكواكب الأخرى قبل ثمان دقائق مضت (أو أياً يكن توقيت سفر الزمن نحو الكوكب الموجود في السؤال) مختلفةٌ بدرجةٍ كافيةٍ عن الأرصاد التي أجريناها منذ قرن، والتي كانت لتبتّ بعدم صحّة النظرية النسبية مباشرة. يحتاج هذا التأثير -في حال كانت نظرية نيوتن صحيحة- أن تكون سرعة الجاذبية مساويةً لعشرين مليار ضعف سرعة الضوء على الأقل!
لكن هناك جزءً آخر من اللغز
تُقوم الأرض -طالما أنها تتحرك أيضاً- بما يشبه "ركوب" هذه الموجات المتحركة في الفضاء، وبذلك تكون دوماً في نقطةٍ مختلفةٍ عن تلك التي انطلقت منها، يبدو الأمر وكأنه لدينا تأثيران متزامنان: تؤثر سرعة كلّ جسم على ما يُعانيه من جاذبية، وكذلك الأمر بالنسبة للتغيرات التي تحدث في الحقول الثقالية.

إن المذهل في القضية، هو أن التغيرات الحاصلة في الحقل الثقالي يتم استشعارها بسرعةٍ محدودةٍ من قِبل الجاذبية، وتأثيرات التفاعلات المعتمدة على السرعة تفني بعضها تقريباً!
عدم وجود هذا الإفناء هو ما يسمح لنا -رصدياً- بتحديد فيما إذا كان نموذج نيوتن (لا نهائي السرعة) هو الصحيح، أو نموذج أينشتاين (سرعة الجاذبية = سرعة الضوء) هو الصحيح والمطابق لكوننا.
نعرف نظرياً أن سرعة الجاذبية يجب أن تكون نفس سرعة الضوء، لكن قوة جاذبية الشمس التي نشعرها، ضعيفة جداً على أن يتم قياس هذا التأثير. في الحقيقة، من الصعب جداً قياسها لأنه إذا كان جسمٌ ما يتحرك بسرعةٍ ثابتةٍ وفي حقل جاذبيةٍ ثابت، لن يكون هناك أي عامل متأثر على الإطلاق. وما نُريده في الحالة المثالية هو نظامٌ يمتلك جسماً يتحرك بسرعةٍ متغيرةٍ داخل حقل جاذبيةٍ متغير؛ فماذا يتطلب ذلك؟
شيئاً كثيفًاً مثل نجمٍ نيوترونيٍّ يدور حول جسمٍ آخر نجمي الكتلة وبقربٍ شديد! في بعض الأحيان نكون محظوظين جداً، ويُصدر النجم النيوتروني ومضاتٍ منتظمةً من الضوء، تُومض بدقةٍ لا تصدق، وهذا ما يجعله نجماً نابضاً (بولزار).
في حالاتٍ نادرةٍ جداً، يُمكننا مشاهدة نجمين نيوترونيين يدوران حول بعضهما البعض! إذا ما كان أحد تلك النجوم النيوترونية بولزاراً يتجه نحونا، يُمكننا حينها اختبار فيما إذا كانت الجاذبية تتحرك بسرعة الضوء أم لا! وبشكلٍ لا يُصدق، اكتشفنا بضعة أنظمةٍ ثنائيةٍ متعددةٍ مكونة من بولزارات تتمتع بهذا التشكيل.
لا يتحرك المصدر الثقالي (star#1) فقط، وإنما الجسم الآخر (star#2) تتغير سرعته أثناء تغيير اتجاهه على مداره حول المصدر الثقالي! (الفيديو)
وعلى نحوٍ لافتٍ للنظر، يتسبب هذا التأثير في تفكك المدار ببطء شديد، ما يقود إلى تغيراتٍ في زمن النبضات!
تنبؤات النسبية العامة حساسةٌ بدرجةٍ عاليةٍ لسرعة الضوء، لدرجة تحسسها لذلك الناجم عن نظام البولزارات PSR 1913+16 (أو ثنائية تايلور-هولس)، حيث تمكنّا من حساب سرعة الجاذبية، ووجدناها مساويةً لسرعة الضوء بخطأ في القياس بلغ 0.2%!
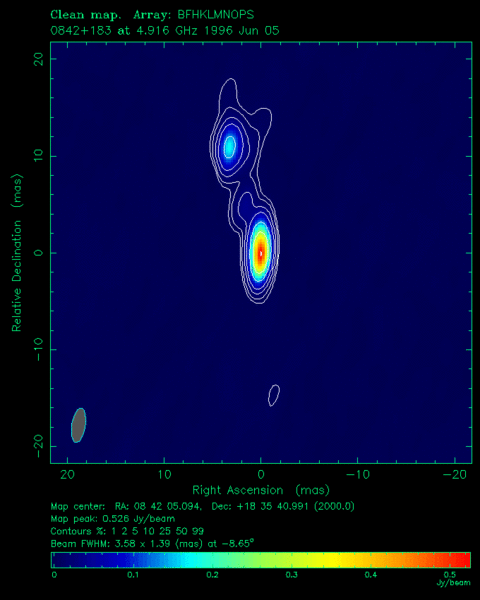
تمكنّا في العام 2002 من إجراء قياسٍ أكثر مباشرةً عندما سنحت لنا الفرصة، جراء تحاذي الأرض والمشتري والكوازار الراديوي QSO J0842+1835 مع بعضهم في الوقت نفسه!
مع تحرك المشتري بين الأرض والكوازار، فإن الانحناء الثقالي للمشتري سمح لنا بقياس سرعة الجاذبية، واستبعاد خيار السرعة اللانهائية وتقدير سرعة الجاذبية بقيمة بين \(2.55×10^8\) و\(3.81×10^8 \)متر في الثانية الواحدة، وهو أمرٌ يتفق كلياً مع تنبؤات أينشتاين. لكن ما نود أن نكون قادرين على فعله حقاً هو الكشف المباشر عن هذه الأمواج الثقالية.
سيكون لدى هوائي الفضاء لقياس التداخل باستخدام الليزر (LISA) الحساسية اللازمة لقياس هذه الأنواع من الأمواج الثقالية، وربما قاس سرعة الجاذبية مباشرةً. إذا ما كنت قد سألت عن هذا الأمر في العقد الماضي، سأخبرك أن LISA يجب أن يأخذ البيانات في العام 2018. لكن لسوء الحظ، سحبت ناسا المشروع في العام 2011، ويبدو الأمر وكأنه لن يصبح واقعاً، على الأقل ليس في الأعوام العشرين القادمة، ما لم يتغير شيءٌ ما.
إذاً وحتى الآن، كل ما حصل هو قياساتٌ غير مباشرة قادمة من أنظمة بولزارات نادرة جداً وتُعطينا أدق القيود، وتُخبرنا أن سرعة الجاذبية هي بين \(2.993×10^8\) و\(3.003×10^8 \)متر في الثانية، وهو تأكيد مذل للنسبية العامة، وصعوبة حقيقية تواجهها النظريات البديلة للجاذبية التي لا يُمكن اختزالها لتصير النسبية العامة! (آسف نيوتن!)
والآن أنت لا تعرف سرعة الجاذبية فقط، وإنما تعلم أيضاً أين يمكنك البحث عنها لتستطيع استيعابها.