تعاون مهندس جامعة نورثويسترن Northwestern إريك لويجتن Erik Luijten مع زبيغنيو روزينيك Zbigniew Rozynek لحل أحد اﻷلغاز عندما التقيا.
عرض روزينيك، وهو باحث في جامعة آدم ميكيويتز Adam Mickiewicz البولندية، شيئًا بدا كالسحر. فعندما وضع قطبًا كهربائيًا إبريّ الشكل في خليط من الجزيئات المعدنية كروية الشكل وميكروية الحجم المنتشرة في زيت السيليكون، التصق أحد الجسيمات في نهاية القطب. وبينما هَمّ روزينيك بإخراج القطب من الخليط التصقت كرة أخرى بالكرة الأولى، ثم التصقت كرة أخرى بالكرة الثانية، وهكذا حتى تشكلت سلسلة طويلة من الكرات.
يقول لوجتن Luijten، وهو أستاذ في علم المواد والهندسة والرياضيات التطبيقية في جامعة نورثوسترن Northwestern: "تصرفت الجسيمات كخرزات مغناطيسية، بالرغم من عدم وجود مغناطيس"، ويضيف: "لم ترد الجسيمات التجمع، فأدركت أن شيئًا أكثر تعقيدًا يحصل".
دمج روزينك، جنبًا إلى جنب مع شركائه فيليب دوتكا Filip Dutka، وبيوتر غارستيكي Piotr Garstecki، وأركاديوس جوزيفزاك Arkadiusz Józefczak، ولوجتن فِرقَهم بهدف فهم الظاهرة التي تسبّبت بتشكيل هذه السلاسل. ويمكن أن يُفضي اكتشافهم إلى إنتاج جيل جديد من الأجهزة الالكترونية والوصول إلى طريقة سريعة وبسيطة لطباعة الدوائر الإلكترونية ثنائية الأبعاد.
وقال روزينيك: "قد تفتح النتائجُ العلمية التي توصلنا لها مجالات أخرى لبحوثٍ مستقبليةٍ، أساسية وتطبيقية"، وأضاف: "ونعمل حاليًا بالفعل على مشاريع مبنيّة على اكتشافنا".
نُشرت الأبحاث على اﻹنترنت اليوم في مجلة نيتشر كميونيكيشنز Nature Communications، وذلك بدعم من مؤسسة العلوم البولندية Foundation for Polish Science، ومركز العلوم الوطني البولندي Polish National Science Centre، والمؤسسة الوطنية الأمريكية للعلوم US National Science Foundation. روزينيك و لوجتن مؤلفان مشاركان، لكن روزينيك مؤلف مشارك أول مع مينغ هان Ming Han أيضًا، وهو طالب دكتوراه في أحد مختبرات لوجتن.
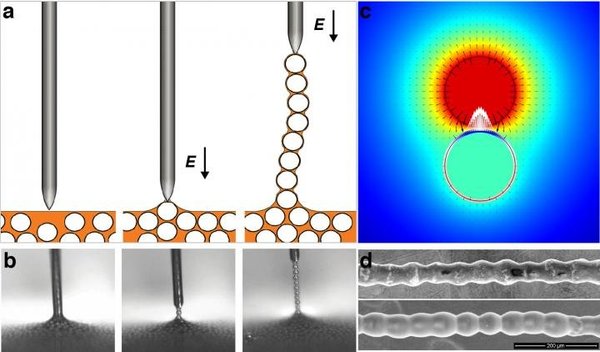
أجرى روزينيك وهان حسابات متعددة، تُبيِّن كيف يُغيِّر حقل القطب الكهربائي خصائص الجسيمات عندما ينزلق القطب في محلول غروي colloidal solution، حيث يستقطب طرفه المشحون كل الجسيمات. وتسبب هذه التفاعلات ثنائية القطب ربط الجسيمات الكروية معًا. ويمكن أن تحتوي السلسلة الناتجة، التي يمكن أن يصل طولها لـ30 سم، على مئات الآلاف من الجسيمات الكروية.
بعد أن حلّ الفريق سر كيفية تشكيل السلاسل، كان لديه سر ثانٍ لكشفه. قال هان: "هناك أمر رائع آخر، وهو أنه لا يلزم حقل كهربائي ﻹبقاء السلسلة متماسكة بعد سحبها من الخليط، حيث أنه بعد إيقاف الحقل تبقى السلسلة المستقرة ثابتة".
بعد أشهر من البحث، اكتشف فريق لويجتن وروزينك أن السلاسل حافظت على هياكلها بسبب 'الجسور' السائلة بين الجسيمات المتجاورة. كلما سحب الباحثون سلسلة من السائل، يعلق زيت السيليكون على جانبي الجسيمات كلها، مشكلًا إطارًا حول كامل السلسلة ومحافظًا عليها سليمة.
وقال هان: "إن التوتر السطحي يلعب دورًا كبيرًا هنا، فقد أدى الجسرُ السائل إلى التصاق الجسيمات ببعضها. الفيزياء هنا مثيرة للاهتمام حقًا، حيث يعتقد معظم الناس أن تطبيق مجال كهربائي هو أمر ضروري لإبقاء الهيكل متماسكًا، ولكنا لا نحتاج لمثل هذا في نظامنا".
عندما تُسحب السلسلة المرنة وتخرج من السائل، يمكن جرّها على الفور على طول السطح لتُنشئ نمطًا. ويعتقد الباحثون بإمكانية استخدام هذه الطريقة كوسيلة بديلة لإنشاء دوائر إلكترونية بسيطة ثنائية البعد، كما يمكن استخدام هذه الطريقة لبناء الهياكل ثلاثية الأبعاد، والتي تتعقد أشكالها عندما يبرد الشمع ويتصلب إذا استُخدم الشمع المنصهر بدلًا من زيت السيليكون.
وقال روزينيك: "على الرغم من بساطة أسلوبنا في تصنيع الهياكل الغروية، إلا أنه أنيق جدًا ويمكن استخدامه في العديد من التطبيقات، بما في ذلك تصنيع مسارات توصيلية تَستخدم ركائز مختلفة، على سبيل المثال، في التطبيقات الإلكترونية".
يعتقد لويجتن وروزينك أن حلّ هذا اللغز يمكن أن يفتح الباب أمام التطبيقات التي لا يمكن التنبؤ بها اليوم. من خلال فهم كيفية عمل الطريقة، فإنها يمكن أن تحدِّد بشكل أفضل كيفية تأثير الأنواع المختلفة من السوائل أو مستويات الجهد على السلاسل وتغيير النتيجة.
وقال لويجتن: "إن فهم طريقة عملها يسهِّل كثيرًا علينا التلاعب بها وتحسينها. يمكننا أن نقول إن الطريقة ستعمل بشكل أفضل أو أسوأ إذا كانت الجسيمات أكبر أو إذا كان المجال الكهربائي أقوى، وهذا ممكن فقط لأننا نفهمها، وإلا سيكون عليك دراسة مجموعات لا نهاية لها".

