برزت مؤخرًا نتيجةٌ غريبة جدًا على الساحة، وتقول أنه إذا قمت بإضافة كل الأعداد الطبيعية \(1+2+3+4\) … فإن الإجابة ستكون 1/12-. ظهرت الفكرة في فيديو لـ Numberphile (انظر أدناه)، والذي يزعمون فيه أنهم برهنوا هذه النتيجة، كما يقولون أن هذه القيمة مستخدمة في كثير من موضوعات الفيزياء.
وجد العامة هذه الفكرة مذهلة جدًا لدرجة أن هذا الموضوع ذُكر في صحيفة New York Times. إذًا ماذا يعني كل هذا؟
طريقة الحساب
يجب أن تعلم، بادئ ذي بدء، أن الجمع اللامنتهي لكل الأعداد الطبيعية لا يساوي 1/12-. تستطيع أن تقتنع بذلك بسهولة إذا ضغطت أزرار آلتك الحاسبة وأدخلت المجاميع الجزئية التالية:
\(S_1 =1\)
\(S_2 =1+2=3\)
\(S_3 =1+2+3=6\)
\(S_4 =1+2+3+4=10\)
…
\(S_n =1+2+3+4+...+n\)،
تستمر \(S_n\) بالازدياد كلما ازدادت \(n\)، أي كلما أضفت أعدادًا طبيعية أكثر. في الحقيقة، فإنه يمكن أن تجعل \(S_n\) كبيرة قدر ما تشاء باختيارك لـ\(n\) كبيرة كفاية. على سبيل المثال، إذا كانت قيمة \(n=1000\)، تحصل على \(S_n=500,500\)، وإذا كانت قيمة \(n=100,000\)، تحصل على \(S_n=5,000,050,000\).
لذلك يقول علماء الرياضيات أن المجموع: \(1+2+3+4+...\) "يتباعد" حتى اللانهاية. ولو وضعناها في كلمات فضفاضة أكثر، نقول أن هذا المجموع "يساوي" اللانهاية.
إذًا من أين أتت القيمة 1/12-؟ هذه النتيجة الخاطئة ظهرت في عمل عالم الرياضيات الهندي المشهور سرينفاسا رامانجن Srinivasa Ramanujan عام 1913. ولكن رامانجن كان يدرك ماذا يفعل، وكان له سبب لكتابتها. كان وقتها يعمل على ما يعرف بـ"دالة زيتا لأويلر" Euler zeta function. لتفهم ماذا يعني ذلك، انظر أولًا إلى المجموع اللامنتهي التالي:
\(S=1+{1 \over 4}+{1 \over 9}+{1 \over 16}+...\)
تستطيع رؤية أن هذا المجموع هو نفسه الذي تحصل عليه عندما تأخذ كل عدد طبيعي، وتربعه، ثم تأخذ مقلوبه:
\(S=1+{1 \over 2^{2}}+{1 \over 3^{2}}+{1 \over 4^{2}}+...\)
هذا المجموع لا يتباعد؛ فإنك إذا أخذت سلسلة من المجاميع الجزئية، كما فعلنا في الأعلى، ستحصل على
\(S_1=1\)
\(S_2=1+{1 \over 2^{ 2}}={5\over 4}=1.25\)
\(S_3=1+{1 \over 2^{ 2}}+{1 \over 3^{ 2}}={49 \over 36}=1.361...\)
…
\( S_n=1+{1 \over 2^{ 2}}+{1 \over 3^{ 2}}+...+{1 \over n^{ 2}}\)
وبعد ذلك تقترب النتائج جدًا من القيمة \( {\pi^{ 2} \over 6}=1.644934 ...\)، بدون أن تتخطاها. يقول علماء الرياضيات أن النتائج "تتقارب" لتصل إلى قيمة \( {\pi^{ 2} \over 6}\)، وبكلمات فضفاضة، فإن هذا المجموع "يساوي" \( {\pi^{ 2} \over 6}\).
والآن ماذا سيحدث لو أنك، بدلًا من رفع المقام إلى القوة 2، رفعته إلى قوة أخرى، ولنقل \( x\)؟ يتضح أن المجموع
\( S(x)=1+{1 \over 2^x}+{1 \over 3^x}+{1 \over 4^x}+...\)
يتقارب ليصل إلى قيمة منتهية، ما دامت قيمة \(x\) أكبر من الواحد. لكل \(x>1\)، يوجد للمجموع \(S(x)\) قيمةٌ معرفة ومنتهية. تعرف \(S(x)\) على أنها "دالة"، وهذه الدالة بالذات تدعى "دالة زيتا لأويلر"، وسميت على اسم عالم رياضيات القرن السابع عشر، ذي الإنتاج العلمي الغزير، ليونهارت أويلر Leonhard Euler.
حسنًا، هذا جيد، ولكن ماذا سيحدث لو أنك وضعت قيمة لـ\( x\) أقل من 1؟ ماذا سيحدث لو أنك وضعت قيمة \(x=-1\)؟ لنرى.
\( S(-1)=1+{1 \over 2^{-1}}+{1 \over 3^{-1}}+{1 \over 4^{ -1}}+...\)
\( =1+2+3+4+...\)
إذًا، سنحصل على مجموعنا الأصلي مرة أخرى والذي، كما تعلم؛ يتباعد. هذا هو الحال بالنسبة لأية قيمة أخرى لـ\( x\) تكون أقل من أو تساوي 1؛ المجموع سيتباعد.
تمديد دالة زيتا لأويلر
تعرّف دالة زيتا لأويلر \( S(x)\) على الأعداد الحقيقية \( x\) والأكبر من 1. الأعداد الحقيقية جزءٌ من مجموعة أكبر من الأعداد اسمها "الأعداد المركبة" complex numbers؛ فبينما تمثل الأعداد الحقيقية جميع النقاط الموجودة على خط ذي طول غير منتهٍ، فإن الأعداد المركبة تمثل جميع النقاط الموجودة على مستوًى، وهذا المستوى يشتمل على خط الأعداد الحقيقية آنف الذكر. هذا المستوى يسمى بالمستوى المركب. بنفس الطريقة التي تقوم فيها بتعريف الدوال التي تحتوي على أعداد حقيقية، يمكنك أيضًا تعريف دوال تحتوي على أعداد مركبة.
أحد الأمور المدهشة عن دوال الأعداد المركبة هو أنه إذا أحاط علمك بالدالة بشكل جيد لمجموعة من المدخلات، فإنه يمكنك أن تعلم قيمة الدالة في الأماكن الأخرى على هذا المستوى المركب. هذه الطريقة في تمديد تعريف دالة ما تعرف باسم "الامتداد التحليلي" analytic continuation. تعرّف دالة زيتا لأويلر على الأرقام الحقيقية الأكبر من الواحد. بما أن الأعداد الحقيقية تعتبر أيضًا أعدادًا مركبة، يمكننا أن نعتبر هذه الدالة دالةً مركبة ومن ثم نطبق الامتداد التحليلي لنحصل على دالة جديدة، معرفةً على مدى المستوى كله ومتوافقةً مع دالة زيتا لأويلر للأعداد الحقيقية الأكبر من الواحد. هذه هي دالة زيتا لريمان.
ولكن هناك أمرًا آخر يمكنك القيام به؛ فباستخدام بعض من الرياضيات عالية المستوى، والتي تدعى "التحليل المركب" complex analysis (انظر الصندوق)، يمكنك تمديد تعريف دالة زيتا لأويلر شاملةً الأرقام \( x\) الأقل من والمساوية للواحد بطريقة تجعلها تعطي نتائج منتهية. بكلمات أخرى، هناك طريقة لتعريف دالة جديدة، ولنسمها \( \zeta(x)\)، بحيث أنه إذا كانت \( x>1\):
\( \zeta (x)=S(x)=1+{1 \over 2^x}+{1 \over 3^x}+{1 \over 4^x}+...\)
وإذا كانت \( x \leq 1\)، يكون للدالة \( \zeta(x)\) قيمة معرفة ومنتهية. هذه الطريقة من التمديد تسمى بـ"الامتداد التحليلي" (analytic continuation)، والدالة الجديدة التي تحصل عليها تدعى بـ"دالة زيتا لريمان" (Riemann zeta function)، تيمنًا بعالم رياضيات القرن الثامن عشر "برنارد ريمان" (Bernhard Riemann). (صياغة هذه الدالة الجديدة والتي تعطي قيما منتهية لـ\( x \leq 1\) تتضمن طرح مجموع متباعد آخر (من المجموع المتباعد الأول)، بحيث أن ناتج طرح "اللانهاية" الناتجة عن المجموع المتباعد الثاني من اللانهاية الناتجة عن المجموع المتباعد الأول سيكون قيمةً منتهية).
حسنًا، والآن لدينا الدالة \(\zeta(s)\) والتي تتفق مع دالة زيتا لأويلر \( S(x)\) عندما تكون القيم الموضوعة أكبر من الواحد. إذا قمت بوضع قيم \( x \leq 1\)، تعطيك دالة زيتا نتيجة منتهية. ما الذي سيحدث لو وضعت \(x = -1\) في دالة زيتا؟ لقد حزرت، النتيجة هي:
\(\zeta(-1)={{-1} \over12}\).
إذا اعتقدت الآن -مخطئًا- أن \(\zeta (x)= S(x)\) عندما \(x=-1\)، فإنك ستحصل على العبارة الخاطئة:
\(S(-1) = 1+2+3+4+...=\zeta(-1)={{-1} \over12}\).
هذه إحدى الطرق التي تجعل من عبارة رامانجن الغامضة أمرًا منطقيًا.
ما هي الخدعة هنا؟
إذًا كيف "أثبت" معدّوا فيديو Numberphile أن الأعداد الطبيعية تُجمع حتى يصل المجموع إلى 1/12-؟ الإجابة الحقيقية هي أنهم لم يفعلوا. مشاهدتهم في هذا الفيديو هو أشبه بمشاهدة ساحر يحاول أن يخرج أرنبًا من قبعة. الخطوة الأولى من "الإثبات" تحاول أن تقنعك بشيء سخيف إلى حد ما، وهو أن المجموع غير المنتهي
\(1-1+1-1+1...\)
يساوي 1/2.
لا يقف الفيديو كثيرًا عند هذه النقطة ويحاول أن يوحي أنها نقطة واضحة. ولكن لننظر عن كثب ونرى إن كانت منطقية أو لا. لنفترض أن المجموع \(1-1+1-1+1-1...\) له قيمة منتهية، ولنقل إنها \(Z\). بإضافة \(Z\) إلى نفسها تحصل على المجموع اللامنتهي التالي:
\(Z+Z=1-1+1-1+1-...+1-1+1-1+1-...\)
ولكن هذا هو نفسه المجموع الأول، ما يعني أن
\(Z+Z=2Z=Z\).
وبما أن \(Z={1 \over 2}\)، فهذا يعني أن \( {1 \over 2}=1\)، الأمر الذي يعد هراءً، وبالتالي فإن التأكيد على أن المجموع غير المنتهي \(1-1+1-1+1-1...\) يمكن اعتباره مساويًا لـ1/2 هو تأكيد ليس بصحيح. في الحقيقة، يمكنك أن تشتق أي نوع تريد من النتائج عن طريق التلاعب بالمجاميع اللامنتهية والتي تتباعد. هذه خدعة!
هذه النتيجة في الفيزياء
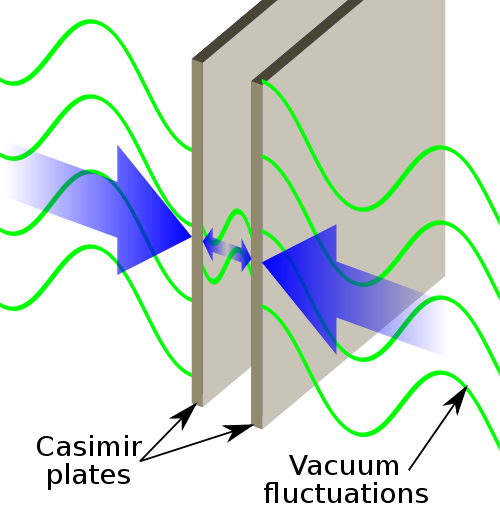
ولكن كيف وجدت هذه النتيجة اللافتة طريقها إلى كتب الفيزياء، كما يظهر الفيديو؟ وهنا تصير الأمور ممتعة. لنفترض أنك أخذت صفيحتين معدنيتين موصِلتين وصففتهما في الفراغ بحيث تكونان متوازيتان. بحسب الفيزياء الكلاسيكية، يجب أن تكون محصلة القوى العاملة بين الصفيحتين تساوي صفرًا.
ولكن الفيزياء الكلاسيكية لا تأخذ في اعتبارها الأثر الغريب الذي تراه عندما ننظر إلى عالم الأجزاء الصغيرة جدًا. لتقوم بذلك، عليك باستخدام فيزياء الكم، والتي تخبرنا بأشياء غريبة جدًا، وأحد هذه الأشياء هو أن الفراغ ليس خاليًا، ولكنه ممتلئ بالنشاط. ما يسمى بـ"الجسيمات الافتراضية" virtual particles تظهر إلى الوجود وتغادره طوال الوقت. هذا النوع من النشاط يعطي ما يعرف بـ"طاقة النقطة صفر" zero point energy: وهو أن الحد الأدنى من الطاقة الذي يمكن أن يمتلكه جسم ما لا يمكن أن يساوي الصفر.
عندما تحاول حساب الكثافة الكلية للطاقة بين الصفيحتين مستخدمًا الرياضيات في الفيزياء الكمية، تحصل على المجموع غير المنتهي:
\(1+8+27+64+...\)
هذا المجموع المنتهي هو نفسه الذي تحصل عليه عندما تضع قيمة \(x=-3\) في دالة زيتا لأويلر:
\(S(-3) = 1+{1 \over {2^{-3}}}+{1 \over {3^{-3}}}+{1 \over {4^{-3}}}+... = 1+8+27+64+...\)
إنه لأمر مؤسف، ﻷن هذا المجموع يتباعد (بسرعة أكبر حتى من \(S(-1)\))، والذي قد يوحي بوجود كثافة لا منتهية من الطاقة. وهذا يعتبر هراءً، كما هو واضح. ولكن ماذا إذا كنت جريئًا واعتبرت أن المجموع اللامنتهي يساوي دالة زيتا لريمان، وليس دالة زيتا لأويلر، معرّفة عند القيمة \(x=-3\)؟ حسنًا، عندها سوف تحصل على كثافة "منتهية" للطاقة. هذا يعني أنه يجب أن تكون هناك قوة جذب بين الصفيحتين المعدنيتين، الأمر الذي يبدو سخيفًا أيضًا، ﻷن الفيزياء الكلاسيكية تفترض عدم وجود أي قوة بينهما.
ولكن إليك مفاجأة. عندما قام علماء الفيزياء بالتجربة وجدوا أن ثمة قوة موجودة – وهي تتوافق مع كثافة طاقة تساوي تمامًا \(\zeta(-3)\)!
هذه النتيجة الفيزيائية المفاجئة تعرف باسم "تأثير كازيمير" (Casimir effect)، مسماة باسم عالم الفيزياء الهولندي "هيندريك كازيمير" (Hendrik Casimir).
خذ لحظة لاستيعاب ذلك. تفترض فيزياء الكم أن كثافة الطاقة يجب أن تكون
\(S(-3)=1+8+27+64+...\)
هذا غير منطقي، ولكن التجارب تظهر أنك إذا نظرت (مخطئًا) إلى هذا المجموع على أنه \(\zeta(x)\) عندما \(x=-3\)، فإنك تحصل على الإجابة الصحيحة. وبالتالي فإنه يبدو أن الطبيعة قد اتبعت الأفكار التي وضحناها في الأعلى؛ فهي قد مددت دالة زيتا لأويلر لتجعلها تحتوي على قيم \(x\) الأقل من 1، وذلك بطرح "اللانهاية" منها بشكل ذكي، وبالتالي حصلنا على قيمة منتهية. هذا أمر مدهش!
السبب في أننا نرى \(\zeta(-1)\) و \( S(-1)\) في فيديو Numberphile وفي كتب الفيزياء، بدلًا من \(\zeta(-3)\) و\(S(-3)\)، هو أنه إذا تخيلت تأثير كازيمير حادثًا في بُعد واحد (على طول خط، وليس في الأبعاد الثلاثة)، ستكون كثافة الطاقة المحسوبة هي \( \zeta(-1)\) بدلًا من \(\zeta(-3)\).
إذًا لماذا نشر معدو الفيديو هذه "النتيجة" الغريبة؟ لا بد حتمًا أن يكونوا يعرفون عن الامتداد التحليلي والذي يجعل من الدالة دالة معرفة، ولكن هذا الأمر كان أمرًا أعقد من أن يُعرض في فيديو. كان من شأن استخدام الامتداد التحليلي أن يجعل من نتيجتهم نتيجة مقبولة، ولكنهم مضوا في الشرح بخفة يدين، مخبأين هذه الطريقة عنا في جيوبهم الخلفية. بفعلهم هذا، فقد حصلوا على مليون مشاهدة، وجعلوا العالم يتحدث عن دالة زيتا وعن الرياضيات، وفي الحقيقة، يجب تهنئتهم على صنيعهم هذا. إن الرياضيات الخاصة بدالة زيتا لهي رياضيات مذهلة، وما شرحنا عنه هنا لا يعدو كونه البداية لقائمة طويلة من الخصائص الرياضية المذهلة.
عندما نريد أن نقدم الفيزياء والرياضيات للعامة، يجب علينا دومًا أن نختار أيَّ المواضيع نترك، وأيَّ المواضيع نشرح، أما عن مكان رسم الخط الفاصل بينهما، فهو أمر يجب تركه لعقلنا اللاواعي ليحدده.