قدمنا لكم في المقال السابق فكرةً عن العمليات الفيزيائية التي تستغلها الحواسيب الكمومية لتكون أقوى من تلك العادية. هل سيكون هذا الاستغلال -لو كان ممكناً بناء حواسيب كمومية كبيرة- قوياً كفايةً لإجراء مهام مفيدة؟ في الوقت الذي لا تزال فيه هذه الإمكانية بعيدةً عقوداً من الزمن، إلا أن الناس يفهمون الكثير عندما يتعلق الأمر بنظرية الحساب الكمومي.
باستخدام رياضيات ميكانيكا الكمّ وعلم المنطق، فإنك تستطيع اكتشاف ما هي إمكانيات الخوارزميات الكمومية (Quantum algorithms)، حتى لو لم يكن لديك حاسوبٌ فعلي. سنلقي في هذه المقالة نظرةً على واحدةٍ من تلك الخوارزميات بتفصيلٍ كبير: إنها النسخة الأبسط لواحدة طوّرها كل من دويتش وجوزسا، وجرى نقاشها في المقال السابق؛ وللاطلاع عليها فلست بحاجةٍ لرياضيات ميكانيك الكمّ، فنحن سنوجهك خلال الخوارزمية لفهمها ونُعطيك المعلومات التي تحتاجها على طول الطريق.
بوابة مهمة جداً
من بين الحقائق المهمة في علوم الحاسوب العادي، هي أن الخوارزمية التي قد تكون حلمت بها يُمكن تطبيقها باستخدام مجموعةٍ من البوابات المنطقية (logic gates) الصغيرة؛ وكما يُشير اسمها، فهذه الدارات الكهربائية مزودةٌ ببواباتٍ مصممةٍ لأخذ بتٍّ أو اثنين كدخل، وإنتاج بتٍّ جديدٍ كخرج. وكمثالٍ على ذلك، يُمكنك مشاهدة الصورة المرافقة.
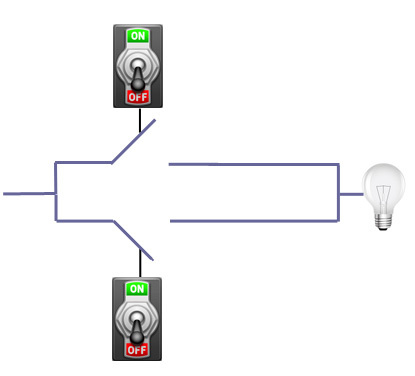
الأمر ذاته صحيحٌ بالنسبة للحساب الكمومي quantun computing، فمجموعةٌ مكونةٌ من عددٍ صغيرٍ من البوابات الكمومية، تكون كافيةً لبناء خوارزميةٍ كمومية؛ وقد تم إثبات هذا الأمر رياضياً. تُعرف إحدى أهم تلك المجموعات ببوابة هادامارد (Hadamard gate)، وفي الواقع يُمكن صنعها (انظر إلى هذا المقال للحصول على تفاصيل).
عندما تستقبل بوابة هادامارد بتاً كمومياً موجوداً في الحالة 0 كدخلٍ لها، فإنها تُعطي بتاً كمومياً جديداً كخرجٍ مكونٍ من حالة تراكب بين 0 و 1، أي الاثنين معاً في الوقت نفسه.
مع ذلك، فإن تلك الحالة عبارةٌ عن تراكبٍ عادي؛ فكما ذكرنا في المقال السابق، عندما تقيس نظاماً ما موجود في حالة تراكب، فإنه ينهار، وتستطيع حينها رصد مخرجاتٍ محددة. وإذا قست خرج بوابة هادامارد بعد استقبالها لبتٍّ كمومي -بحالة 0- فهناك احتمالية 50:50 لتُشاهد 0 أو 1؛ وللفيزيائيين طريقتهم التالية في كتابة التراكب (superposition):
\(\frac{1} {\sqrt 2} |0\rangle+\frac{1} {\sqrt 2} |1\rangle. \)
التعابير \( |0\rangle \) و\( |1\rangle \) يُشيران إلى كون حالة البت الكمومي إما 0 أو 1، وإشارة الجمع هي إشارةٌ توضح أنه لدينا حالة تراكبٍ لاحتماليتين. لكن لماذا يوجد مع كل حدٍّ من الحدين (\({1}/ {\sqrt 2} \))، بدلاً من 1/2، القيمة التي تتعلق باحتمالية الرصد؟
ستأخذنا الإجابة للغوص عميقاً في ألغاز ميكانيكا الكمّ، ولذلك دعنا نُقدم الفكرة: نتعامل في الحياة العادية مع الاحتمالات، وهي دوماً أعدادٌ موجبة، ومجموع جميع الاحتمالات الممكنة (مثل مشاهدة 0 أو 1) هو دائماً 1. في ميكانيكا الكمّ هناك مفهومٌ أكثر عموميةً للتعبير عن القصة، ويُعرف ذلك المفهوم بالسعة الاحتمالية ( probability amplitude)، التي من الممكن أن تكون سالبة، وفي الواقع فإن تلك السعات عبارةٌ عن أرقام عقدية.
ليس من المطلوب أن يكون مجموع السعات الاحتمالية لكل الاحتمالات مساوٍ لواحد، لكن ذلك مطلوبٌ بالنسبة لمجموع مربعاتها. والعوامل الموجودة في علاقتنا في الأعلى تُمثل السعات، وهي تُحقق العلاقة التالية:
\( (\frac{1} {\sqrt 2} )^2 +(\frac{1} {\sqrt 2} )^2 =1/2+1/2=1 \)
ترتبط السعات مع الاحتمالات عبر عملية التربيع، فاحتمال رؤية خرجٍ محددٍ عندما تُجري قياساً ما، هو مربع القيمة المطلقة للسعة المرافقة. ولذلك، ففي مثالنا المذكور في الأعلى، تكون القيمة \({1}/ {\sqrt 2} \) مرتبطةً بالاحتمال المساوي لـ 1/2.
عندما نُغذي بوابة هادامارد ببتٍّ في الحالة فهو لا يمر. عندما يكون البت الكمومي في الحالة 1 فهو يعبر البوابة، وفي الوقت نفسه يصير في حالة تراكبٍ من 0 و 1، لكن في هذه الحالة بسعة مساوية لـ \(| 1\rangle \) وهي سالبة:
\(\frac{1} {\sqrt 2} |0\rangle-\frac{1} {\sqrt 2} |1\rangle. \)
كيف يختلف هذا الأمر عن الحالة التي نضع فيها 0؟ إن مجموع مربعات السعات هو نفسه في الحالتين، ولذلك فإن القياس يُعطينا 50:50 لمشاهدة 0 أو 1 في كِلا الحالتين. يكمن الاختلاف في كيفية تطوّر الحالتين بمرور الزمن وتفاعلهما مع الحالات الأخرى (أو البتّات الكمومية).
السعات الاحتمالية هي أعدادٌ معقدةٌ تحتوي معلوماتٍ أكثر من تلك الموجودة فقط في عددٍ موجبٍ مفرد. وبشكلٍ من الأشكال، فإن كل الغموض الذي يكتنف ميكانيكا الكمّ، كالظواهر الغريبة مثل التراكب التي لا نشاهدها في عالمنا اليومي، يختفي في تلك المعلومات الإضافية.
التداخل
تُعطينا بوابة هادامارد أيضاً مثالاً جيداً عن ظاهرةٍ أخرى مهمةٍ بالنسبة للحساب الكمومي، وتُعرف بالتداخل. لمعرفة كيفية عمل هذه الظاهرة، دع \( |0\rangle\) يمر عبر بوابة هادامارد للوصول إلى التراكب التالي:
\(\frac{1} {\sqrt 2} |0\rangle+\frac{1} {\sqrt 2} |1\rangle. \)
ماذا سيحصل لذلك إذا مرّرناها عبر بوابة هادامارد مجدداً؟ لحسن الحظ، فإن الطبيعة لطيفةٌ عندما يتعلق الأمر بالرياضيات اللازمة لعمل تلك الظاهرة، وهي سهلة جداً. يُمكننا إجراء ذلك دون أي مقدمات، فببساطة، نُطبق الصيغة الموجودة في الأعلى، والتي تُخبرنا ما ستفعله البوابة للحالتين \( |0\rangle\) و\( |1\rangle\)، وهذا يؤدي إلى:
\(\frac{1} {\sqrt 2} \left(\! \frac{1} {\sqrt 2} |0\rangle+\frac{1} {\sqrt 2} |1\rangle \!\right) +\frac{1} {\sqrt 2} \left(\! \frac{1} {\sqrt 2} |0\rangle-\frac{1} {\sqrt 2} |1\rangle \!\right) \)
بعد فك هذين القوسين، من السهل معرفة أن الحدين \(|0\rangle \) يُلغيان بعضهما البعض، ليتبقى لدينا
\(\frac{1} {2} |0\rangle+\frac{1} {2} |0\rangle=|0\rangle \)
التعبير \(|0\rangle \) الموجود في هذه المعادلة هو إشارة لـ 1، ما يعني أنه إذا قسنا البتّ الكمومي الآن، فإننا سنحصل على 0 بشكلٍ مؤكد.

ظاهرة التداخل هي بالتحديد عملية الإلغاء هذه، أو إضافة الحدود. هناك تداخلٌ هدّام (destructive interference)، حيث تقوم حدود \(|1\rangle\) في مثالنا بإلغاء بعضها البعض، وبالتالي يختفي الحد من المعادلة. وهناك أيضاً تداخلٌ بنّاء (constructive interference)، حيث تُضاف الحدود إلى بعضها، وهذا ما حصل مع الحد \(|0\rangle\) في مثالنا. غالباً ما يفكر الناس بهذه الحدود على أنها أمواجٌ يُمكنها التداخل بشكلٍ بنّاء أو هدّام.
التداخل يعني أن البدء بالحالة \(|0\rangle\) وتطبيقها لمرتين على بوابة هادامارد سيُعطيك من جديد الحالة الابتدائية \(|0\rangle\)
\( |0\rangle\rightarrow\frac{1} {\sqrt 2} |0\rangle+\frac{1} {\sqrt 2} |1\rangle \rightarrow |0\rangle \)
يُمكنك إقناع نفسك بأن نهجاً مماثلاً سيُعطينا التالي بالنسبة للحالة \( |1\rangle \)
\( |1\rangle\rightarrow\frac{1} {\sqrt 2} |0\rangle-\frac{1} {\sqrt 2} |1\rangle \rightarrow |1\rangle \)
مثال
دعنا الآن نعُد إلى الخوارزمية التي طوّرها كلٌ من دويتش وجوزسا، والتي استخدمناها كمثالٍ في المقال السابق. كانت المهمة في فحص فيما إذا كان تابعٌ ما سيأخذ سلسلة بتات مكونة من واحداتٍ أو أصفار كدخلٍ مستقر ومتوازن. الاستقرار يعني أن التابع يأخذ نفس القيمة 0 أو 1 لكل المحارف.
أما التوازن فيعني أنه يُسند القيمة 1 إلى نصف المحارف تماماً، والقيمة 0 إلى النصف الآخر. الحالة الأبسط هي عندما تكون المحارف -التي تُشكل دخل التابع- عبارة عن بت طويل جداً. وسيكون التابع الثابت إما:
\(f(1)=0\) و \(f(0)=0\)
أو
\(f(1)=1\) و \(f(1)=0\)
والتابع المتوازن سيكون إما
\(f(1)=0\) و \(f(0)=1\)
أو
\(f(1)=1\) و \(f(0)=0\)
إذا كنت تعمل مع حاسوبٍ عادي، سيجد برنامجٌ ما فيما إذا كان التابع الثابت أو المستقر بحاجةٍ إلى استرجاع قيم التابع لمرتين، أي مرة لفحص قيمته 0، وأخرى من أجل 1. لا توجد طريقة سريعة للإجابة عن سؤالك، وما برهنه كل من دويتش وجوزسا في العام 1992 هو وجود خوارزميةٍ كموميةٍ قادرة على استرجاع قيمة التابع لكلٍّ من الصفر والواحد في الوقت نفسه، ومن ثمّ إخبارك فيما إذا كان التابع مستقراً أو متوازناً.
الفكرة العامة
تستخدم الخوارزمية حقيقتين بسيطتين. تتضمن الحقيقة الأولى حالة التراكب:
\(\frac{1} {\sqrt 2} |0\rangle-\frac{1} {\sqrt 2} |1\rangle=\frac{|0\rangle-|1\rangle}{ {\sqrt 2}}\)
يُمكنك تغيير هذه الحالة إلى سالبة ببساطة، عبر إضافة 1 إلى كل مركبة، وذلك باستخدام الجمع الثنائي، الذي يعني أن 1+1 لا يساوي 2 وإنما 0. ويُعطي هذا:
\(\frac{|0+1\rangle-|1+1\rangle} {\sqrt 2} =\frac{|1\rangle -|0\rangle} {\sqrt 2} =-\frac{|1\rangle -|0\rangle} {\sqrt 2} \)
سنبقي هذه العلاقة في أذهاننا كطريقةٍ محتملةٍ لتغيير الإشارات.
الحقيقة الثانية المستخدمة هي واحدة رأيناها سابقاً، وتتضمن قدرة بوابة هادامارد على تغيير حالات التراكب
\(\frac{|1\rangle -|0\rangle} {\sqrt 2} \) و \(\frac{|1\rangle+|0\rangle} {\sqrt 2} \)
إلى صفرٍ وواحدٍ على التوالي.
الآن افترض أننا نتعامل مع حالة تراكب شبيهة، لكن إشارة السعتين تُحدد بواسطة قيم التابع f. ودعنا ندعو هذه الحالة\(| \psi \rangle \)
\(| \psi \rangle=\frac{(-1)^{f(0)}|0\rangle+(-1)^{f(1)}|1\rangle}{\sqrt2} \)
تُشير هذه العلاقة إلى أن سعة \(|0\rangle\) تمتلك إشارةً سالبةً إذا كان \(f(0)=1\)، وموجبةً إذا كان \(f(0)=0\). الأمر نفسه صحيحٌ بالنسبة للحالة \(|1\rangle\)، وبالتالي سيكون التابع الثابت على الشكل
\(| \psi \rangle=\pm \frac{|0\rangle+|1\rangle} {\sqrt 2} \)
والتابع المتوازن
\(| \psi \rangle=\pm \frac{|0\rangle-|1\rangle} {\sqrt 2} \)
عندما نطبق بوابة هادامارد على الحالة \(| \psi \rangle\)، فإن الإشارات تعبر العملية ببساطة. وسينتج عن التابع الثابت إما \(|0\rangle\) أو \(-|0\rangle\). ومهما كانت النتيجة، فعندما تُجري قياساً ما، فإنك ستحصل حتماً على 0.
ينتج عن التابع المتوازن إما \(|1\rangle\) أو \(-|1\rangle\). ومهما كانت النتيجة، فإنّ أي عملية قياسٍ ستُعطي حتماً القيمة 1. وبالتالي، إذا تمكنت من إنتاج الحالة \(| \psi \rangle\) بطريقةٍ ما، فإن بوابة هادامارد ستُقدم لنا إجابةً عن سؤالنا المتعلق فيما إذا كان التابع ثابتاً أو متوزاناً. هذه الإجابة ستكون قاطعة.
الخوارزمية
دعونا الآن نجمع كل تلك المعلومات معاً، ونُشاهد كيف تعمل الخوارزمية. ولأنها تعتمد على حقيقتين، فقد لا تتفاجأ باستخدامها لبتّين كموميين. في البداية، لاحظ أنه للإجابة عن السؤال المتعلق بطبيعة التابع f (ثابت أم متوازن)، وفيما إذا كان بإمكاننا القيام بذلك كلاسيكياً أم علينا استخدام الحساب الكمومي، فإننا بحاجةٍ لافتراض أن الحاسوب يمتلك طريقةً ما لاسترجاع أو حساب قيم f ليُقدم 0 أو 1 اللذين يحتاجهما لإيجاد\(f(0)\) أو \(f(1)\).
وهذا الأمر هو شيء تعاملنا معه على أنه مُعطى، ولذلك السبب ندعو هذه الطريقة بالصندوق الأسود (black box): نحن نعرف ما يقوم به، لكننا لسنا مهتمين بكيفية إنجازه للعمل.
وفي الوقت نفسه، يُمكننا الافتراض أننا نمتلك صندوقاً أسود يعمل بقطعتين من المعلومات، مُسجل الدخل ومُسجل الخرج. في حالة البتات الكلاسيكية، فإن مسجل عملية الدخل يضع القيمة i (التي هي إما 0 أو 1) ومُسجل الدخل القيمة j (التي هي 0 أو 1 أيضاً)، ويحسب الصندوق الأسود القيمة \(f(i)\) ويُضيفها إلى j ليُعطينا كخرج القيمة \(j+f(i)\).
عملية الجمع هنا هي ثنائية، وصندوقنا ما هو إلا طريقةٌ أخرى تُخبرنا بقيمة \(f(i)\) بدلالة الإجابة عن سؤالنا، وهذا الأمر لا يُشكل أيّ فرق، إذ أننا لا نزال بحاجةٍ إلى استخدام الصندوق مرتين، لتحديد فيما إذا كان التابع ثابتاً أو متوازناً.
في السياق الكمومي، فإن المُسجلات هي البتات الكمومية، ويُمثل الصندوق الأسود البوابة الكمومية التي تُحول النظام المكون من بتين هما \(|i\rangle\) و \(|j\rangle\) إلى \(|i\rangle\) و\(|j+f(i)\rangle\).
إليك بعض الحيل الرياضية، فلإنتاج الحالة \( \psi \) نُطبق على الصندوق الدخل
\(\frac{|0\rangle+|1\rangle} {\sqrt 2} \)
ومُسجل الخرج سيكون
\(\frac{|0\rangle-|1\rangle} {\sqrt 2} \)
سيجري تحويل الدخل إلى الحالة \( \psi \)، ولا يتضمن ذلك أكثر من تغيير الإشارة (بالاعتماد على f)، وسيجري هذا الأمر بمساعدة مُسجل الخرج، القادر على إنجاز هذه المهمة كما شرحنا سابقاً. وحالما تُنتج الحالة \(| \psi \rangle\) بهذه الطريقة -باستخدام الصندوق الأسود لمرةٍ واحدة- فإنه بإمكاننا وببساطةٍ استعمال بوابة هادامارد لمعرفة فيما إذا كان التابع متوازناً أو ثابتاً.
الحسابات
للبرهنة على قدرة صندوقنا الأسود على إنجاز الأمر بشكلٍ سليم، سنستفيد من حقيقةٍ مهمةٍ جداً، وهي إمكانية تمثيل النظام ثنائي البت رياضياً كعملية ضرب:
\( \left(\frac{|0\rangle+1\rangle} {\sqrt 2} \right) \left(\frac{|0\rangle-1\rangle} {\sqrt 2} \right) \)
والتي يُمكن كتابتها
\( \frac{1}{\sqrt 2}\left(|0\rangle\frac{|0\rangle+1\rangle} {\sqrt 2} +|1\rangle\frac{|0\rangle-1\rangle} {\sqrt 2} \right) \)
ولمعرفة ما سيفعله الصندوق الأسود للحد
\(|0\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \)
يُمكننا ببساطة مشاهدة ما سيفعله بالنسبة لكل مركبةٍ من مركبات التراكب \(|0\rangle-|1\rangle\)، وذلك يُعطينا
\(|0\rangle\frac{(|0+f(0)\rangle-|0+f(0)\rangle)} {\sqrt 2} \)
وعندما يكون \(f(0)=0\)، نحصل على
\(|0\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \)
لكن عندما \(f(0)=1\)، فإن ذلك يعني وفقاً لما ذكرناه من حقائق في الأعلى
\(|0\rangle\frac{-(|0\rangle-|1\rangle)} {\sqrt 2} \)
وبجمع هاتين المعادلتين معاً، فإن ذلك يُقدم لنا التعبير التالي:
\((-1)^{f(0)}|0\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \)
وبشكلٍ مشابهٍ لما سبق، فإن الصندوق الأسود يُحول التعبير
\(|0\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \)
إلى
\((-1)^{f(1)}|1\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \)
وبتعويض (2) و (3) في (1)، فإننا نحصل على
\(\frac{1}{\sqrt 2} \left((-1)^{f(0)}|0\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2}+(-1)^{f(1)}|1\rangle\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \right) \)
\(= \left(\frac {(-1)^{f(0)}|0\rangle+(-1)^{f(1)}|1\rangle}{\sqrt 2} \right) \left(\frac{(|0\rangle-|1\rangle)} {\sqrt 2} \right) \)
\(= \psi \frac{(|0\rangle-|1\rangle)} {\sqrt 2}\)
وتُمثل هذه الحالة ما نبحث عنه.
مثّلت خوارزمية جوزسا ودويتش إنجازاً، لأنها كانت أول خوارزميةٍ كموميةٍ أفضل من الخوارزمية الكلاسيكية، فهي تحتاج إلى عمليةٍ واحدةٍ لمعرفة قيم التابع (في الوقت نفسه لكلا القيمتين 0 و 1) بدلاً من اثنتين.
بعد ذلك، عمّم الباحثون هذه الخوارزمية لتعمل مع التوابع التي لا تأخذ فقط أصفاراً وواحداتٍ كدخل، وإنما سلسلةً من المحارف المكونة منها (انظر المقال السابق)، وبرهنوا على أنه في هذه الحالة ستكون الخوارزمية الكمومية أسرع بشكلٍ أسيٍّ مقارنةً بمثيلتها الكلاسيكية.
هذا ممتعٌ جداً، لكن هل له أي استخدام؟ المشكلة التي تحلها خوارزمية جوزسا ودويتش ليست مفيدةً في الواقع بالنسبة للعالم الحقيقي. ما هي المهام الأخرى التي يُمكن لميكانيكا الكمّ إنجازها بشكلٍ أفضل من الطرق الكلاسيكية؟ وكم نبعد عن امتلاكنا لحواسيب كمومية وظيفية؟ هي أسئلةٌ سنُجيب عنها في مقالاتٍ أخرى.
مؤلفة المقال
ماريان فرايبيرغر Marianne Freiberger محررة في "بلس". وتود شكر (ريتشارد جوزسا)، و (لاي ترابنل) بروفيسور الفيزياء الكمومية في جامعة كامبريدج لمساعدته القيمة وصبره في تقديم الشروحات العامة والقيمة.


