عالمٌ فصاميٌّ يُحارِب الفصاميةَ الكلاسيكية
تنطلقُ معظم مراجع ميكانيكا الكمّ من علاقات أينشتاين-بلانك (Planck-Einstein relations)، وقد يصعب علينا كثيراً إيجاد كتب تُدرِّسُ ميكانيك الكم ولا تنطلق من هذه العلاقات، تتعامل هذه العلاقات مع التفاعلات الحاصلة بين الأمواج والمادة على أنها عمليات مُفردة؛ بمعنى أن الإشعاع الكهرومغناطيسي يظهر مكوَّناً من جسيمات مفردة تُعرف باسم الفوتونات (photons)، وتأخذ هذه العلاقات الشكل التالي:
\(E=hυ ..... (1)\)
\(P ⃗=ℏ.k ⃗ .......(2)\)
حيث يُمثل \(ℏ\) ثابت بلانك المُعدّل، و\(υ\) تردد الموجة، و\(k ⃗\) شعاع الموجة.
من ناحية أخرى هناك ركيزةٌ أساسية في ميكانيك الكم تُعرف بمعادلة شرودينجر، وتثبت التجاربُ التي يُجريها العلماءُ، على نحو مستمرّ، صحّة هذه المعادلة، على الرُّغم من عدم قدرة أي شخص حتى يومنا هذا على اشتقاق هذه المعادلة أو البرهان على صحتها نظرياً، وهو أمر دفع العالمَ العظيم ريتشارد فاينمان إلى القول بأنّ مناقشة هذه القضية هي مضيعة للوقت، وهذه المعادلة إنما جاءت ببساطة من عقل شرودينجر، وتأخذ معادلة شرودينجر الشكل العام الآتي:
\(iℏ {∂\over {∂t}} ψ(r ⃗,t)={-ℏ^2\over2m}∆ψ(r ⃗,t)+V(r ⃗,t)ψ(r ⃗,t)\)
تمتازُ هذه المعادلة بالعديد من الخواصّ المهمة، التي ترسم بينها وبين غيرها من المعادلات الموجودة في الميكانيك الكلاسيكي خطوطاً عريضة جداً، وفي هذه المعادلة يُمثّلُ \(ψ(r ⃗,t)\) ما يُعرف بالتابع الموجي (wave function)، ولازال تفسير هذا التابع ومعناه الفيزيائي محط جدل ونقاش بين كثير من العلماء، لكنّ الحقيقة الثابتة في ميكانيك الكم تُخبرنا أنّ علينا ترك كلّ شيء يتعّلق بالحدس السليم والخبرات اليومية والتسلح بالرياضيّات فقط ، عند الوصول إلى هذه المعادلة.
تحكم هذه المعادلة سلوك الأنظمة الميكروسكوبية، والماكروسكوبية أيضاً، التي لا يعود الميكانيك الكلاسيكي قادراً على دراستها والتنبؤ بالظواهر التي تنجبها، بل ويصبح عاجزاً حتى عن تفسير أمور نختبرها في تجربتنا اليومية.
بدايةً، إذا ما كان لدينا جسيم ما، فإن مجرد ذكرنا لهذه القضية يعني أنّ احتمال وجود هذا الجسيم في حجمٍ مساوٍ للكون هو 1، وهذا الأمر واضح جداً بالنسبة لنا، لكن كيف سيكون الأمر عند الحديث عن حجمٍ أو منطقة ما مُحددة، وبماذا يُساعدني التابع الموجي؟
عند الحديث بمنطق الرياضيّات، يمتاز التابع الموجي \(ψ(r ⃗,t)\) الذي نُشاهده في معادلة شرودينجر بعددٍ من الخصائص المهمة جداً، وسنذكر أهمها هنا وهي تلك التي ستساعدنا في فهم الصورة الفصامية لنموذج بور، وأيضاً في فهم قوة مبدأ الارتياب (uncertainty principle)، ومن بين أهم خواصّ هذا التابع:
- يحتوي التابع الموجي لجسيم ما كلّ المعلومات التي يُمكن أن نحصل عليها بخصوص هذا الجسيم.
- يُفسَّرُ التابع الموجي \(ψ(r ⃗,t)\) رياضياً على أنه سعةٌ احتمالية لوجود الجسيم، وعند الحديث عن احتمال \(dP(r ⃗,t)\) وجود الجسيم داخل الحجم \(d^3 r\)، نجد أن هذه الاحتمالية تُعطى بـ
\(dP(r ⃗,t) \sim d^3 r=dx.dy.dz\)
ويُمثل \(|ψ(r ⃗,t)|^2\) الكثافة الاحتمالية، وبالتالي يصير احتمال وجود الجسيم داخل الحجم \(d^3 r\) مُعطىً بالعلاقة:
\(dP(r ⃗,t)=c|ψ(r ⃗,t)|^2 d^3 r\)
بالتالي يُمكننا حساب احتمال وجود الجسيم ضمن حجم ما V عبر العلاقة
\(∫_V c|ψ(r ⃗,t)|^2 d^3 r\)
حسناً، تُعتبر السطور السابقة أساس وجوهر ميكانيك الكم، ومنها ينطلق الشخص نحو هذا العالم المنافي لحسّ التجربة والخبرة اليومية، وهذه البداية يُمكن تلخيصها في ثلاث نقاط:
- كل ما يُمكننا الحديث عنه في ميكانيكا الكم هو التنبؤ بالاحتمالات فقط.
- في عالم ميكانيك الكم تختفي الاستمرارية، ويبدأ الانقطاع بالظهور، فمثلاً لا وجود في ميكانيك الكم لطيف طاقة مستمر، وبالتالي تصدر الجسيمات وتُمتص عند طاقات مُحددة ومعروفة، وحتى الكواكب نفسها لا تتمتع بطيف طاقة مستمر على الإطلاق، ولكن ما يجعلنا نشعر بوجود طيف الطاقة المستمر في العالم الماكروسكوبي الكبير هو قيمة ثابت بلانك الصغيرة جداً، مما يجعل من السويات الطاقية المتاحة لجسم ما قريبة جداً من بعضها ويصعب بالتالي علينا الفصل بينها وهنا نفترض الاستمرارية، ولذلك ليس من الغريب أبداً أنّ نيوتن لم يبدأ اكتشافاته بميكانيك الكم وإنما بالميكانيك الكلاسيكي، فالإنسان غالباً ما ينزع لدراسة ما تُشاهده حواسه وما يختبره يومياً، وبعدها ينطلق ليُحلل عوالم أخرى (حاول حساب السويات الطاقية المتاحة لكوكب الأرض أثناء دورانه حول الشمس).
- في ميكانيك الكم، هناك أهمية كبيرة لما يُعرف بثنائية الجسيم-الموجة، فلكل جسيم موجة تُرافقه.
نظرة عن قرب إلى التابع الموجي
تكلمنا في المقاطع السابقة عن أنّ التابع الموجي يحتوي كل المعلومات التي يُمكن أن تكون موجودة عن جسيم ما، وقُلنا إنه يُفسر على أنه سعة احتمالية، وهذا ما يُعرف حقيقةً بتفسير كوبنهاغن الذي قاده نلز بور ومؤيدوه.
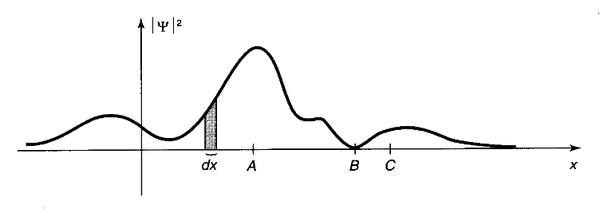
لننسى في هذه الأثناء ميكانيك الكم قليلاً، ولنتذكر فقط أن مربع طويلة التابع الموجي يُمثل الكثافة الاحتمالية لإيجاد الجسيم في منطقة ما –أو مجرد تابع كثافة احتمالية فقط دون أي إسقاط فيزيائي. الآن، لنفترض أن تابع الكثافة الاحتمالية هذا يتغير وفقاً للشكل الموجود في الأسفل، إذاً ما الذي يعنيه هذا الشكل علماً أن x تُمثل الإحداثي الخاص بحركة جسيم تتم في بعدٍ واحد؟
يُخبرنا منحني تابع الكثافة الاحتمالية السابق ومباشرةً أن احتمال وجود الجسيم بجوار النقطة A هو أكبر ما يُمكن، في حين يكون هذا الاحتمال أصغر ما يُمكن بالقرب من B.
يُمكنني أيضاً وبشكلٍ مباشر ملاحظة أمر آخر، وهو أن مربع الكثافة الاحتمالية هو عدد حقيقي أكبر من الصفر دوماً، وهذا الأمر يلعب دوراً مهماً جداً في ميكانيك الكم، وهذا ما سنتطرق إليه في مقالات عميقة لاحقة لأن هذه الصفة تلعب دور الساحر في عالم الجسيمات العنصرية وميكانيك الكم.
بالعودة الآن إلى التابع الموجي، نجد أن التفسير الاحتمالي له يقترن دوماً بعدم تعيين (indeterminacy)، بمعنى حتى لو عرفت كل شيء يُمكن أن تخبرك إياه النظرية عن الجسيم، لن تستطيع أبداً أن تتنبأ بخرج تجربة بسيطة بتحديد تام، وكل ما يُمكنك القيام به هو إعطاء تفسيرات إحصائية احتمالية لمخرجات محتملة للتجربة.
هذه الصفة الملازمة لميكانيك الكم لم تدفع علماء الفيزياء فقط إلى الجنون، وإنما الفلاسفة أيضاً، فهي تتناقض وبشكلٍ صارخ مع قواعد الفيزياء الكلاسيكية الحتمية بطبعها، والتي تُخبرك بإمكانية التحديد المطلق لحالة نظام ما حالما عرفت قيم المتحولات التي تصفه، ولا تترك الفيزياء الكلاسيكية مكاناً للشك؛ فلو عرفت كمية حركة جسيم وموقعه في لحظة ما، فإنه –وفقاً للميكانيك الكلاسيكي- يُمكنك تحديد مساره المستقبلي بدقة متناهية، وكذلك دراسة تاريخه السابق، أي لا وجود لعدم تعيين هنا وهذا أمرٌ يُعد في عداد المستحيلات في ميكانيك الكم.
حسناً، هل عدم التعيين هذا هو صفة أصيلة في الطبيعة، أم أنه مجرد خطأ في القياس؟
للإجابة عن السؤال السابق، افترض أنك أجريت قياساً لموقع جسيم ووجدته في النقطة C، حينها سيأخذ السؤال السابق الصيغة التالية: "أين كان الجسيم قبل قياس وجوده في النقطة C"، ستساعدنا هذه الصيغة المغايرة شكلاً، والمطابقة مضموناً في الإجابة عن السؤال السابق.
يُمكن سرد ثلاث وجهات نظر هنا؛ وأولى وجهات النظر، أو الإجابات، تلك دعا إليها اينشتاين ووفقاً لها فالجسيم كان في C، وهذه الإجابة تنسف ميكانيك الكم كاملاً وتجعل منه نظريةً غير مُكتملة، وتطرح الفكرة القائلة بأن عدم التعيين ليس جزءاً من الطبيعة وإنما هو مجرد انعكاس لجهلنا، وكان ديسبانا أكثر تطرفاً في تبنيه لوجهة النظر هذه، إذ قال: "لم يكن موقع الجسيم غير محدد على الإطلاق، وإنما مجهول للمُجرب فقط"؛ وتبعاً لهذه الإجابة لا يُمثل التابع الموجي كل شيء يُمكن معرفته عن الجسيم، بل هناك متحولات مختفية hidden variables لازمة لتقديم الوصف الكامل للجسيم. هل هذه الإجابة صحيحة؟
قبل الحكم، لنتعرف على إجابات أخرى. تقول الإجابة الثانية، التي قد تبدو غريبة للوهلة الأولى وقد تستمر غرابتها على مدى فترة طويلة من تعلمك ودراستك لميكانيك الكم، أن الجسيم لم يكن في أي مكان في الحقيقة، إنها جملة كفيلة حقاً بدفع ليس علماء الفيزياء فقط، وإنما أعظم الفلاسفة إلى التهام أوراقهم وربما الاستعاضة عن ممارسة العلم، بالرقص أو الغناء.
ووفقاً لوجهة النظر هذه، فإنّ فعل القياس هو من أدى إلى إجبار الجسيم على الوجود، أما السؤال عن كيفية وسبب وجوده في C، فهي في عداد الأسئلة التي لا نجرؤ على طرحها، ولنتركها جانباً –حالياً على الأقل.
كان جوردان واضحاً جداً في هذه النقطة، وقد عبّر بكل صراحة عن أنّ "عمليات الرصد لا تقوم فقط بالتسبب في اضطراب الجملة التي نقيسها، بل تُنتجها أيضاً. ونحن من يُجبر الجسيم على أخذ موقع محدد". عُرفت وجهة النظر هذه بتفسير كوبنهاغن، ولو كانت صحيحة فهي تقترح وجود شيء ما غريب جداً يتعلق بفعل القياس (measurement act)، وهو شيء دفع إلى نقاش وجدل استمر على أكثر من نصف قرن؛ وسنعود إلى هذه القضية في مقالاتٍ لاحقة، وسنتناولها بتفصيلها الرياضي ونتلمس المعادلات التي ستساعدنا على فهم الأمر كاملاً.
هناك إجابة ثالثة مٌقترحة وهي ببساطة رفض الإجابة عن السؤال. ليست وجهة النظر هذه سطحية كما تبدو للوهلة الأولى، إذ قد يبدو من غير المنطقي الحديث عن أي شيء قبل عملية القياس، لأن هذه العملية هي من اعطاني معلومة عن وجود الجسيم في النقطة C، وبالتالي وفقاً لوجهة النظر هذه لا وُجود لما يُعرف بـ "قبل القياس"، وبالتالي ربما يكون الرفض منطقي، أو القول: "لا أدري".
كان لكلٍ من وجهات النظر تلك مؤيدين من علماء الفيزياء، لكنّ الأمر تغير عند مجيء عالم الفيزياء جون بيل في العام 1964، الذي استبعد الإجابة الثالثة، وجعل الخيار قائم بين الإجابتين الأولى (اينشتاين) والثانية (تفسير كوبنهاغن). في الحقيقة، وعند الأخذ بعين الاعتبار لنظرية بيل (Bell theorem) –لن نناقشها الآن لأننا لا نملك الأدوات اللازمة لذلك، وسنؤجل الأمر إلى مقالات لاحقة- ينتصر تفسير كوبنهاغن.
يُمكننا تلخيص النقاش السابق بالسطور التالية: لا يمتلك الجسيم أي موقع محدد بدقة قبل إجراء القياس وهو شبيه لموجة تنتشر في حوض، وعملية القياس هي من أدى إلى ظهور عدد محدد، وبالتالي خلقت شعوراً بوجود نتيجة محددة، لكن لا يجب نسيان أنّ هذه النتيجة مقيدة بوزنها الإحصائي الناجم عن الطبيعة الاحتمالية للتابع الموجي.
الأذكياء لا يغيبون أبداً عن عالم الفيزياء، وسيظهر أحدهم مستعجلاً ليسأل محاولاً تدمير نتيجة بيل، فيقول: ماذا لو أجريناً قياساً ثانياً وفي الحال وراء القياس الأول، هل سنحصل على C أيضاً، ام أنّ فعل القياس سيؤدي إلى حصولي على رقم آخر تماماً في كل مرة أجري فيها القياس؟
في الحقيقة يتفق الجميع هنا، على أنّ القياس المُكرر للجسيم نفسه لا بدّ أن يقود إلى القيمة نفسها، أي C. وهنا تماماً، سيسأل ذلك "الذكي" كيف أمكن لتفسير كوبنهاغن أن يتصدى لحقيقة أن القياس التالي سيُعطي C أيضاً؟
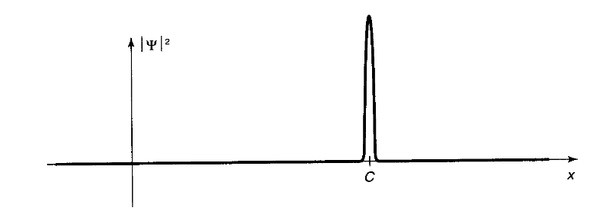
يُجيب تفسير كوبنهاغن على هذه النقطة بالقول أن القياس أثّر وبشكلٍ مباشر على التابع الموجي للجسيم، ليصل إلى القمة في النقطة C (كما هو موضح في الشكل التالي)؛ ونقول حينها أنّ التابع الموجي انهار جرّاء فعل القياس –هذا الانهيار سيُناقش رياضياً في مقالات لاحقة والوقت مبكر جداً على نقاشه هنا- ليصل إلى الذروة المتمركزة حول C؛ وللحصول على نفس القيمة في قياس تالي، يجب إجراء القياس بسرعة كبيرة لأن التابع الموجي سيتابع الانتشار وفقاً لمعادلة شرودينجر مجدداً.
حسناً إليك خلاصة تفسير كوبنهاغن: هناك نوعين منفصلين تماماً من العمليات الفيزيائية، وهما النوع العادي الذي يتطور فيه التابع الموجي وفقاً لمعادلة شرودينجر، والنوع الثاني "القياس" وفي هذه العمليات ينهار التابع الموجي فجأةً وبشكلٍ غير مستمر –كما هو موضح في الشكل أعلاه.
النموذج المريض لبور
انطلق بور في دراسته للإلكترون الذري بوصفه جسيمًا كلاسيكيًا، لكنه اعتمد الوصفَ الكموميّ لمدارات هذا الإلكترون حول نواته، وبالتالي استخدم مزيجاً من المفاهيم الكمومية والكلاسيكية لوصف مدار الإلكترون حول النواة، واتّبع المحاكاة التالية:
ليكن لدينا إلكترون موجود في مدار دائري نصف قطره r وقيمة كمية حركته \(p=mv\)، وليتخلص من معضلة كلاسيكية تقول أنه وفقاً لنظرية ماكسويل فالالكترون يُشع طاقة وبالتالي ستجه بشكل حلزوني نحو النواة، افترض ليحصل تطابق مع الواقع:
\(pr=nℏ ....... (3)\)
حيث n عدد صحيح.
الآن، حتى نستطيع التحدث عن الإلكترون باستخدام الميكانيك الكلاسيكي، يجب أن يُكون كلٌّ من الارتياب الحاصل في كمية حركته وموقعه صغيرين جداً مقارنةً بـ p وr، أي
\(∆p≪p \)
\(∆x≪r\)
ويُمكننا بناءً على العلاقات السابقة استنتاج أن:
\({∆p \over p} {∆x\over r}≪1 ...... (∗)\)
إذاً، لا بد من تحقق العلاقة السابقة حتى نتمكّن من اعتماد الوصف الكلاسيكي للإلكترون، لكن هل وصفُ بور هذا صحيح؟ وهل يتفق مع ميكانيك الكم، وهل سيجعلُ أيُّ تضارب مع ميكانيك الكم من هذا الوصف الهجين، الذي اعتمد جانباً من ميكانيك الكم وآخر من الميكانيك الكلاسيكي، خاطئاً؟ كيف سنعرف فيما إذا كان هذا الوصف منسجماً تماماً مع ميكانيك الكم؟ ببساطة كلُّ ما علينا عمله هو الاستعانة بالمبدأ "الإلهي": مبدأ الارتياب.
يُخبرنا مبدأ الارتياب أنّ:
\(∆p.∆x≥ℏ\)
وبالتالي:
\({∆p\over p} {∆x\over r}≥{ℏ\over pr}.... (∗∗)\)
وبالاستفادة من العلاقة (3)، يُمكننا كتابة العلاقة (∗∗) على الشكل الآتي:
\({∆p\over p} {∆x\over r}≥{1\over n} .... (∗∗∗)\)
الآن، وحتى يصحَّ وصفُ بور لا بدّ من أن تكون العلاقتان (∗∗∗) و(∗) متوافقتين تماماً، وهنا يظهرُ السؤال التالي: ما مدى التوافق بينهما؟
عندما تكون قيمة n كبيرة جداً، ولنقل "جدلاً" أنها تسعى إلى اللانهاية، وحينها تُصبح العلاقة (∗∗∗) على الشكل التالي -طبعًا الأمر أكثر تعقيدًا من ذلك بكثير وسنعود إليه في حينه:
\({∆p\over p} {∆x\over r}≥0\)
ويبدو لنا أنّ هناك توافقاً كبيراً بينها وبين العلاقة (∗)، فكلما كبرت قيمة n كلما أصبحت صحة العلاقة (∗) كبيرة جداً، لكن وبصرف النظر عن المسمى الحقيقي لـ n في إطار ميكانيك الكم وعن معناه، نُلاحظ مباشرةً أنه عندما تكون قيمتها مساوية لـ 1، فالعلاقة (∗∗∗) تأخذ الشكل:
\({∆p\over p} {∆x\over r}≥1\)
في حين تبقى العلاقة (∗) على حالها، أي:
\({∆p\over p} {∆x\over r}≪1 \)
حسناً، لدينا مشكلة كبيرة هنا، أليس كذلك؟
يظهر التجانس فقط عندما تكون قيمة n أكبرَ بكثير من الواحد؛ لكن حُكما لن نأخذ بفرضية الميكانيك الكلاسيكي وإنما سنخضع مرغمين لصحة مبدأ الارتياب -الذي نُسلم به هنا وسنعود لشرحه فيزيائيًا واستنتاجه رياضيًا أيضا-، وبالتالي علينا التخلي تماماً عن الصورة نصف الكلاسيكية التي اعتمدها بور في دراسته للمدارات الإلكترونية.
ما الذي دفعنا إلى هذا الاستغناء؟ وكيف سنحلُّ هذه الإشكالية؟ وما الذي يُقدمه مبدأ الارتياب لنا هنا؟ في الحقيقة إنه يُعطينا كلّ شيء، إنه يُقدم الحلّ، وهذا ما سنتحدث عنه في المقالة القادمة.
إلى أنْ يحين موعدُ نشر المقال القادم، حاول حلّ المسائل الآتية:
- اكتب معادلة شرودينجر الخاصة بجسيمٍ حرّ في فضاء قيمة الكمون فيه V=0.
- إذا كان لدينا إلكترون في مسرّع جسيمات بطاقة تصل إلى 1 غيغا إلكترون فولط، هل يُمكنك حساب الطول الموجي المرافق لهذا الإلكترون، وهل نعتبره حينها جسيمًا أم موجة؟
- ما هو الطول الموجي لإلكترون يجري تسريعه في حقلٍ كهربائي كمونه V، ومتى يُمكنني رصد ظواهر التداخل (السلوك الموجي) في شبكة بلورية يبلغ البعد بين ذراتها رتبة الإنغستروم.