صورة تجمع بين نيلز بور (على اليمين) وفيرنر هايزنبرغ من عام 1932. حقوق الصورة: Caltech
بقلم رائد شيا، باحث في الفيزياء حاصل على درجة البكالوريوس في الفيزياء من جامعة دمشق عام 2014.
مقدمة
إن تفسير كوبنهاغن هو عبارةٌ عن تفسيرٍ لميكانيكا الكم قام بوضعه بشكل رئيسي كل من نيلز بور (1) وفيرنر هايزنبرغ (2)، وقد أخذ اسمه هذا من مدينة كوبنهاغن عاصمة الدانمارك، التي احتوت على معهد نيلز بور الذي كان يعمل فيه هايزنبرغ مساعداً له (أي لنيلز بور) في حينها.
على الرغم من أنّ هذا التفسير يُعد أحد أكثر التفسيرات شيوعاً بين الفيزيائيين، فهو يعطي صورةً عن الواقع المحيط بنا أغرب من الخيال، وسنحاول في هذا المقال أن نشرح هذا التفسير، محاولين أن نبين ما هي الأسباب التي أجبرت الفيزيائيين على تبني هكذا صورةً غريبة للغاية عن العالم. ولكن لفهم ذلك، لا بد لنا من الحديث عن تجربة تحمل في طياتها غرائب ميكانيكا الكم، محاولين من خلالها أن نوصل لكم الصورة العجيبة للغاية، والتي تجبرنا ميكانيكا الكم أن نرسمها عن العالم.
تجربة الشق المزدوج
تحمل تجربة الشق المزدوج (3) في طياتها أعمق ألغاز ميكانيكا الكم. وقد قال عنها مرةً أحد ألمع الفيزيائيين في التاريخ، والحائز على جائزة نوبل في الفيزياء، الفيزيائي الأمريكي ريتشارد فاينمان (4) ما يلي: "إنه لمن المستحيل ...أن نفسّرها بأية طريقة كلاسيكية، إنها تحتوي جوهر ميكانيكا الكم. إنها في الحقيقة تحتوي على الغموض الفريد ]ميكانيكا الكم[." (5)
غموض ميكانيكا الكم؟ عمّ نتحدث هنا يا ترى؟ نعود لاقتباس ريتشارد فاينمان مرةً أخرى، والذي قال: "أعتقد أنه يمكنني القول مطمئناً، أن لا أحد يفهم ميكانيكا الكم...وحاول إذا ما استطعت لذلك سبيلاً، ألا تقول لنفسك، "ولكن، كيف يمكن أن تكون الأمور على هذا النحو؟" لأنك ستنجرف إلى زقاقٍ مظلم، لم يستطع أحد قبلك الهرب منه. لا أحد يعلم حقاً كيف يمكن للأمور أن تكون على هذا النحو." (6)
إذاً، هل أنت مستعدٌ للغوص في هذا العالم الغريب؟ فلنبدأ.
خلاف حول طبيعة الضوء
مما يتكون الضوء يا ترى؟ لقد اعتقد نيوتن (7) أنّ الضوء يتكون من جسيمات صغيرة يمكن لنا تشبيهها برصاصات صغيرة للغاية، إلا أنّ هايغنز (8) خالفه الرأي، واقترح أنّ الضوء يتكون من أمواج، كالأمواج التي تنتشر على سطح الماء. وقد كانت المسألة غير محسومةٍ حتى أتت تجربة الشقين التي اقترحها توماس يونغ (9) التي يمكن لنا من خلالها حسم هذه المسألة.
في هذه التجربة، نضع منبعاً للضوء بالقرب من حاجزٍ يحتوي على شقين ضيقين، وتليه شاشةٌ نستقبل عليها ما يمرّ من ضوء من خلال الشقين.
لفهم فائدة هذا الإجراء التجريبي، لنتخيل أننا أجرينا التجربة برصاص حقيقي. وأننا وضعنا على الشاشة كواشف لمكان سقوط الرصاصات (أكياس رمل مثلاً). عندها سيظهر على الشاشة النمط المُبين في الرسم التوضيحي التالي:
هذا ليس غريباً البتة. فإما أنّ الرصاصة ستمرّ من أحد الشقين مباشرةً إلى الشاشة دون أن تصطدم بالحاجز أو قد ترتد عن الحاجز أو أنها ستصطدم فيه ليغير مسارها الأصلي نحو إحدى نقاط الشاشة كما في الشكل.
والآن، ماذا لو أجرينا التجربة باستخدام أمواج الماء؟ إن ما نريد قياسه في هذه الحالة هو طاقة الموجة، وما سنبينه على الشاشة هو هذه الطاقة، والتي يمكن قياسها من خلال اهتزاز كرة خفيفة نضعها على الماء. سنلاحظ في هذه الحالة، نمط تداخلٍ مبين في الرسم التوضيحي التالي:
يمكن فهم السبب ببساطة: بما أنّ الموجة تكون عبارةً عن قمم تليها قيعان، وكون الشقين سيعملان كمنبعين جديدين (للعارفين بالفيزياء، مترابطين، ولكن لا يهم الآن للقارئ العادي فهم المعنى الدقيق لذلك)، كما هو مُبين بالشكل، عندها ستتداخل الأمواج الصادرة عن أحد الشقين مع الأمواج الصادرة عن الآخر، وفي أماكن التقاء قمة مع قمة أو قعر مع قعر، سيهتز الماء بشكل أعظمي، ونقول أنّ لدينا حالة تداخلٍ بنّاء، في حين أنه عند التقاء قمة مع قعر، فسيلغيان بعضهما، وسيسكن سطح الماء تقريباً، ونحصل على تداخلٍ هدام، وسيظهر على الشاشة نمط تداخل ثابت مبين في الشكل أعلاه.
بالتالي إذا أنتج الضوء نمط تداخل، فسيكون مكوناً من أمواج. في حين أنه لو لم ينتج نمط تداخل، بل نمطاً يشبه ما ظهر عند إطلاق الرصاصات، فسنعلم أنه مُكون من جسيمات.
بالفعل، تم إجراء التجربة، وكانت نتيجتها أنّ الضوء أعطى نمط تداخل، وبالتالي فهو مُكون من أمواج. وقد تطورت لاحقاً النظرية الموجية للضوء كثيراً بعد اكتشاف معادلات ماكسويل (10)، ليتبين أنّ الضوء هو عبارةٌ عن موجاتٍ كهرومغناطيسية.
قد تظنون أنّ القصة قد حُسمت. وبالفعل، فقد أصبح هذا هو الرأي السائد لفترةٍ من الزمن. إلا أنه في أواخر القرن التاسع عشر، وبدايات القرن العشرين، تم اكتشاف العديد من الظواهر التي لم يمكن تفسيرها من خلال الطبيعة الموجية للضوء، ولكنها فُسرت جيداً من خلال الطبيعة الجسيمية له، ونذكر من هذه الظواهر هنا دون تفصيل، التأثير الكهروضوئي (11)، وتأثير كومبتون (12)، وإشعاع الجسم الأسود (13). أُطلِق على الجسيم المكون للضوء اسم الفوتون.
ما زاد الطين بلة هو اكتشاف أنّ هذه الطبيعة المزدوجة لم تكن خاصة بالضوء وحده، فجميع الجسيمات في الطبيعة، كالإلكترونات على سبيل المثال، تتصرف في بعض الظواهر كأمواج، وفي بعضها الآخر كجسيمات!
فما هي القصة فعلاً؟
إلقاء نظرةٍ جديدةٍ على تجربة الشق المزدوج
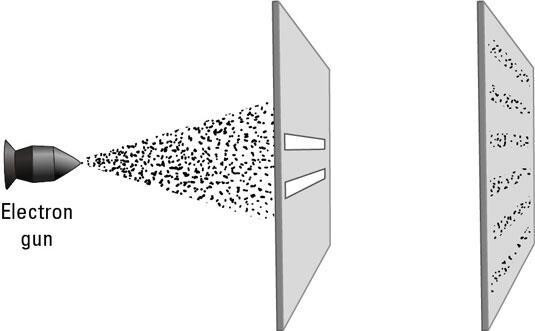
بما أنّ جميع الجسيمات تسلك هذا السلوك، فلنقم بهذه التجربة على منبعٍ يصدر الإلكترونات، ولنقس مكان سقوطها على الشاشة. لنفرض أننا جعلنا شدة المنبع ضعيفةً للغاية، لدرجةٍ تجعله يطلق الإلكترونات بشكلٍ منفرد واحداً تلو الآخر. عندها لو تركنا أحد الشقين فقط مفتوحاً وأغلقنا الآخر، فسنجد أنّ الإلكترونات تسقط في شريطٍ يقابل الشق، كما نتوقع تماماً، وهنا لا يوجد شيءٌ غريب حتى الآن. ولكن ما أن نفتح الشقين معاً، حتى نُصدم بنمطٍ كالمبين في الصورة التوضيحية التالية:
ماذا يحصل؟ كيف يمكن للإلكترونات التي نفترض في العادة أنها انطلقت من المنبع كجسيمات، أن تنتج نمط تداخلٍ كالأمواج؟
تمرّ الإلكترونات واحداً واحداً، أي لا يمكننا القول بأن الإلكترونات تتفاعل مع بعضها لتنتج هذا النمط. فكيف لنا أن نفسر ما نرى؟ كيف يمكن للإلكترون عند مروره من أحد الشقين أن يتأثر سواء كان الشق الثاني مفتوحاً أم لا؟ بل كيف له أن يعلم (مجازياً) أنّ الشقين مفتوحان معاً أو أن أحدهما فقط هو ما تم فتحه؟
هل يمكن أن يكون الإلكترون قد مرّ عبر الشقين معاً وتداخل مع نفسه؟ للتحقق من الفرضية الأخيرة، نضع جهاز قياسٍ عند أحد الشقين كي يكشف لنا مرور الإلكترون عبره. وهنا تحصل المفاجأة الأكبر: عندها يختفي نمط التداخل، ويتصرف الإلكترون كما لو أنه جسيمٌ مجدداً، وكأنه يعلم بأننا نراقبه فقرر عدم التصرف كموجة!
فما الذي يحصل فعلاً؟ إن الإلكترون لا يعلم، وليس لديه عقلٌ كي يقرر طبعاً، فما الذي تفعله الطبيعة خلف الكواليس؟
محاكمة جهاز القياس
هنا، لا بد لنا من التدقيق بالطريقة التي قسنا بها ما إذا مرّ الإلكترون من الشق الأول أو الثاني. تتضمن إحدى طرق القياس أن نضع بين منبع الإلكترونات والحاجز الذي يحوي الشقين منبعاً ضوئياً، كما في الشكل التخطيطي التالي:
الرسم هو مُبسط للغاية، وتمت فيه المبالغة بشكلٍ هائل بالمسافة بين الشقين، ولكن المهم أن تصل الفكرة. الآن، بالنسبة للإلكترونات التي تصل الشاشة، نفترض أنّ ما يمكن أن يحدث هو التالي: إذا مرّ الإلكترون من الشق العلوي، فسيتأثر بالحزمة الضوئية المُبينة في الشكل باللون الأحمر، وسنعلم من هذا أنه مرّ من هذا الشق. في حين لو لم يحصل ذلك، سنفترض أنّ الإلكترون قد مرّ من الشق السفلي. عند إجراء التجربة، يختفي نمط التداخل ويتصرف الإلكترون كجسيمٍ مجدداً. قد يقول قائل، ربما أنّ شدة الحزمة الضوئية قد خربت سلوك الإلكترونات الموجي، وأنّ علينا إضعاف شدتها كثيراً حتى تصبح عبارةً عن مجموعة فوتونات قليلةٍ تخرج تباعاً. ولكن هنا سنواجه مشكلةً جديدةً: فإما أن يتفاعل الفوتون الصادر مع الإلكترون ويقيسه لنا، أو أنّ الإلكترون سيمرّ دون أن يتفاعل مع أيّ فوتونات ولن نتمكن عندها من قياس موضعه، فهل سنحصل في هذه الحالة إذاً على مزيج من نمط التداخل مع النمط الذي يتكون نتيجة تصرف الإلكترون كجسيمٍ عند قياسه بالحزمة الضوئية الشديدة؟ عند إجراء التجربة، نجد أن ذلك ما يحصل حقاً! فما الذي يجري؟
قد يقول قائل أنّ المشكلة في نوع جهاز قياس الشق الذي عبر منه الإلكترون، وأنه علينا تغيير طريقة القياس للتحقق من ذلك. وبالفعل، عند إجراء التجربة، نجد أنه مهما كانت الطريقة المستخدمة لمعرفة الشق الذي مرّ منه الإلكترون، سواء استخدمنا حزمة ضوئية أو حجرة فقاعات (14) أو أي طريقةٍ أخرى، فالنتيجة واحدة: عندما نصمم التجربة بحيث لا نعلم من أي شقٍ سيمرّ الإلكترون، سنجد نمط تداخل على الشاشة وأنّ الإلكترون يتصرف كموجة. في حين أنه عندما نصمم التجربة بحيث نقيس من أي شقٍ مرّ الإلكترون، يختفي نمط التداخل ويتصرف الإلكترون كجسيمٍ مجدداً!
قبل المتابعة، لا بد عند هذه النقطة من تفنيد أسطورةٍ شائعة حول هذه التجربة، والتي تم ترويجها في العديد من المصادر التبسيطية وغير التخصصية التي تتحدث عنها. يوحي البعض عند الحديث عنها بأنّ وجود مراقبٍ واعٍ يقوم بالقياس هو ما يجعل هذا السلوك الغريب يظهر، ولكن كما رأينا فهذا الكلام غير صحيح، إذ أنّ حزمةً ضوئيةً أو حجرة فقاعاتٍ أو أي تجربةٍ فيزيائية تتفاعل مع الإلكترون لتحدد من أي شق مرّ ستؤدي لهذه النتائج الغريبة، ولا عالقة للوعي بالموضوع هنا.
لذلك دعونا نتابع التفكير بطريقةٍ علميةٍ وكما يفترض بنا أن نفعل دائماً، كي نتحرى ما الذي يحصل هنا.
تجربة الخيار المتأخر وازدياد الغرابة (15)
يبدو وكأن الطبيعة تلعب معنا، لذلك فلنأخذ الأمور لمستوً جديدٍ تماماً، ولنضع جهاز القياس بعد الشقين، أي بين الحاجز والشاشة وليس بين منبع الإلكترونات والحاجز، بحيث أنّ عملية القياس تحصل بعد عبور الإلكترونات للحاجز وبالتالي يُفترض أن تتصرف كموجة، ولنرَ ما سيحصل. تُدعى هذه التجربة باسم تجربة الخيار المتأخر، وقد تم إجراؤها فعلاً (لكن بطريقةٍ أعقد مما ذكرناه هنا بالطبع إلا أننا لن ندخل في تفاصيلها). كانت النتيجة أنه حتى في هذه الحالة، اختفى نمط التداخل، وعاد الإلكترون يتصرف كجسيم. أي وكأنّ الإلكترون كان يعلم في الماضي بأننا ننوي في المستقبل وضع جهاز قياسٍ بعد الحاجز، فتصرف على هذا الأساس. وهذا هو السبب الذي جعل البعض يقول بأنّ ميكانيكا الكم تسمح بتأثير الحاضر بالماضي، فوضعنا لجهاز القياس بعد الشقين في الحاضر وبعد أن يكون الإلكترون قد عبر، سيؤثر على سلوك الإلكترون عند عبوره في الماضي!
فهل هذا ما يحصل بالفعل؟ بدأت الأمور تزداد غرابةً بشكل كبير جداً!
الممحاة الكمومية: أغرب من الخيال (16)
لكن، وفي محاولة أخيرة منا لإنقاذ الحسّ السليم، نقول أنه لا يمكن لإلكترون أن يتصرف بناءً على حصولنا على معلوماتٍ عن أي شق قد مرّ منه. ولإثبات ذلك، نقوم بتعديلٍ طفيفٍ على تجربة الخيار المتأخر، وذلك كما يلي: بعد أن يقيس جهاز القياس من أي شقٍ عبر الإلكترون، نضيف للتجربة مرحلةً لاحقةً تمحو المعلومات التي حصل عليها جهاز القياس، بحيث نفقد هذه المعرفة عن مكان مرور الإلكترون. وكون أنّ الإلكترون سيتصرف كجسيم بعد عبوره لجهاز القياس، فنفترض أنّ الأمر سيبقى كذلك ولن نحصل على نمط تداخلٍ من جديد. ولكن ما يحدث هو أمرٌ مهولٌ بالفعل. فبعد أن أجريت هذه التجربة فعلاً، لوحظ أنه بمجرد محو المعلومات عن مكان مرور الإلكترون من أي شقٍ على الحاجز، يعود نمط التداخل ليظهر من جديد، أي أنّ الإلكترون يعود للتصرف كموجة مجدداً!
على ما يبدو فقوانين الطبيعة مُصممة لتحرمنا من هذا النوع من المعرفة (معرفة من أي شق قد عبر الإلكترون فعلاً) وهذا فائق الغرابة. فهل هناك نموذجٌ عقلاني يشرح لنا ما الذي يحصل؟
إعادة النظر في مفهوم الحتمية
قبل ميكانيكا الكم، كان الفيزيائيون ومنذ أيام غاليليو (17) ونيوتن (18) معتادين حول توصيف الطبيعة بقوانين حتمية. معنى ذلك، هو أنه لو كررنا نفس التجربة ضمن نفس الظروف تماماً، فسنحصل على نفس النتائج. مثلاً، فلتتخيل أنك تقوم برمي كرةٍ صغيرة أفقياً من سطح بناءٍ ما، ولنفترض أنّ هذه الكرة صغيرةٌ وكثيفة بحيث نستطيع أن نهمل تأثير الهواء عليها. عندها ففي كل مرةٍ ترمي هذه الكرة من نفس النقطة على البناء وبنفس السرعة والاتجاه، فستسلك نفس المسار عبر الهواء.
فسرت الفيزياء المصوغة وفق قوانين حتمية، والتي ندعوها بالفيزياء الكلاسيكية، كل شيء تقريباً كان معروفاً في حينها من حركة الأجسام على الأرض، إلى حركات الكواكب والأجرام السماوية، إلى الكهرباء والمغناطيسية ...إلخ. بل قد تتفاجأ إذا علمت أنه حتى نظرية النسبية الخاصة والعامة لآينشتاين (19) هي نظرية كلاسيكية تماماً.
فهل نستطيع أن نفسر تجربة الشقين وفق قوانين حتمية؟ دعونا نرى.
إنّ أول درس قاسٍ تعطينا إياه تجربة الشقين، هو أنه علينا التخلي عن أي فكرةٍ لمسارٍ كلاسيكيٍ مُحددٍ تماماً لإلكترون، إذ لو كان الأمر كذلك، لتصرف الإلكترون تماماً كرصاصةٍ نطلقها نحو الحاجز، ولكان قد مرّ من أحد الشقين أو الآخر، وبالتالي لظهر على الشاشة نمط يشبه النمط الذي نحصل عليه بإطلاق الرصاصات، وهو مختلف كل الاختلاف عن نمط التداخل، وهذا يخالف الواقع!
في الحقيقة، لا يقتصر الأمر على ذلك، بل يتعداه لواقعٍ أغرب بكثير.
لنتخيل معاً أنّ الإلكترون يخضع فعلاً لقانونٍ حتمي لا نعلمه. عندها من حيث المبدأ، فهذا القانون سيفرض على الإلكترون شكل مسارٍ محدد تماماً، نستطيع استنتاجه فيما لو عرفنا هذا القانون. ولكن كما رأينا، فإن وجود مسارٍ محدد تماماً لإلكترون بالطريقة الكلاسيكية يتعارض مع ظهور نمط التداخل، وهو ما يخالف الواقع كما رأينا!
هذا يمثل إطلاق رصاصة الرحمة على مفهوم الحتمية ككل، ويبدو أنه علينا أن نتعايش مع حقيقة أن الإلكترون لا يتصرف بشكلٍ حتمي!
هل يعني ذلك أننا لا نستطيع التنبؤ بأي شيءٍ حول سلوك الإلكترون؟ لحسن الحظ، لا. فلنتذكر أنه عندما ظهر نمط التداخل عند إطلاق الإلكترونات فرادى، فقد كان سببه أنّ الإلكترونات كانت تسقط بكثافةٍ عالية في بعض المناطق، وبكثافة منخفضة في مناطق أخرى كما يبين الشكل:
وتعني المناطق التي تحوي كثافةً عاليةً لمواقع سقوط الإلكترونات أنّ احتمال سقوط إلكترون عليها هو احتمال عالٍ نسبياً، والعكس صحيح بالنسبة للمناطق ذات الكثافة المنخفضة. بالتالي، فحتى وإن كنا لا نستطيع التنبؤ بمكان سقوط الإلكترون الوحيد على الشاشة، فنحن نستطيع تحديد احتمال سقوطه على مناطق مختلفة. بالتالي فعلينا أن نصوغ القوانين التي تحكم سلوك الإلكترون بشكل احتمالي بحت، وهذا يمثل ابتعاداً صارخاً للغاية عن روح الفيزياء الكلاسيكية!
التعمق في فهم نمط التداخل
بما أننا قررنا أن نصوغ قوانيننا بشكلٍ احتمالي، فعلينا فهم نمط التداخل الذي ظهر معنا والذي سنستخدمه كدليلٍ في صياغة هذه القوانين.
لنفكر الآن في كيفية ظهور نمط تداخل في الأمواج العادية، كالأمواج المنتشرة على سطح الماء.
كما ذكرنا قبل قليل، فإنّ ما نقيسه هنا ويظهر مُمثلاً على الشاشة هو طاقة الموجة، والتي يمكن قياسها بسهولة من خلال اهتزاز كرةٍ خفيفة موضوعة على سطح الماء. فكيف تكون طاقة الموجة بهذا الشكل؟ إن التفسير في غاية البساطة.
إنّ الموجة في هذه الحالة هي عبارة عن اهتزاز لسطح الماء. لنفرض أننا نقيس الارتفاع بالنسبة إلى سطح الماء. سنفرض أنّ النقاط معدومة الارتفاع هي النقاط على مستوى سطح الماء عندما كان مستقراً قبل أن يبدأ بالاهتزاز. سنعطي النقاط الأعلى من سطح الماء ارتفاعاً موجباً (مثلاً لو كانت النقطة فوق سطح الماء بـ 3 سم سنقول أنّ ارتفاعها هو 3 سم)، أما النقاط الأخفض من سطح الماء فسنعطيها ارتفاعاً سالباً (فلو كانت أخفض من سطح الماء بـ 3 سم مثلاً سنقول أنّ ارتفاعها هو -3 سم).
والآن، عندما تعبر الموجة من الشقين، فإنّ كلاً منهما سيتصرف كمنبعٍ لموجةٍ جديدةٍ كما في الشكل أعاله. وعندما ننظر لنقطة من سطح الماء قرب الشاشة، فسيصلها الاهتزاز من كلا المنبعين (الشقين). فلو وصلتها قمتان لموجتان معاً، فإن ارتفاعها فوق سطح الماء سيكبر (مثلاً لو كانت قمة كل موجة على ارتفاع 3 سم، سيصل ارتفاع النقطة فوق سطح الماء عندما تصلها قمتان معاً إلى 6 سم وسيكون ارتفاعها في هذه الحالة موجباً)، في حين لو وصل للنقطة قعران لموجتين في نفس اللحظة، فستنخفض تحت سطح الماء بشكلٍ كبير (مثلاً لو كان انخفاض أول موجة 3 سم والثانية 3 سم أيضاً فستصبح تحت مستوى سطح الماء الأساسي بـ 6 سم ونقول أنّ ارتفاعها هنا هو -6 سم لأنها تحت مستوى سطح الماء)، ونقول في الحالتين السابقتين أننا حصلنا على تداخل بنّاء. أما لو وصلت للنقطة قمة موجة من المنبع الأول مع قعر موجةٍ من الثاني، فلن تهتز أبداً (فالموجة الأولى تحاول رفعها بمقدار 3 سم في حين تحاول الموجة الثانية خفضها بمقدار 3 سم وبالتالي ستلغي الموجتان بعضهما وتبقى النقطة عند سطح الماء وارتفاعها عنه بالتالي معدوم)، أي أننا حصلنا في هذه الحالة على تداخلٍ هدام.
لكن هل لذلك علاقةٌ بطاقة الموجة؟ في الواقع، نعم. ترتبط طاقة الموجة بمربع ارتفاعها، أي حاصل ضربه بنفسه. لذلك سنجد أنّ طاقة الموجة تكون عظمى في كلتا حالتي التداخل البناء المذكورتين أعاله، في حين ستكون صغرى في حالة التداخل الهدام. ولأنّ قمم الأمواج وقعورها ستتداخل وفق ما شرحناه أعاله في نقاط عديدة على سطح الماء، فسيظهر نمط التداخل الذي نشاهده في الصورة.
أمواج الاحتمال (20)
لكن، كيف يمكن لنا الاستفادة مما سبق لتفسير تجربة الشق المزدوج؟ إن ما يلعب دور طاقة الموجة في مثال الماء، هو احتمال أن يسقط الإلكترون في مكان معين على الشاشة. لذلك يمكننا أن نفسر ما نرى إذا افترضنا أنّ ما يصف سلوك الإلكترون هو موجة، يعبر مربع سعتها (السعة هي مصطلح يقابل الارتفاع في حالة أمواج الماء) عن احتمال رصد الإلكترون في نقطة ما على الشاشة، وهذه الموجة هي ما تتداخل مع نفسها لتعطينا النمط الذي نشاهده في تجربة الشق المزدوج.
إن هذا الأمر رائعٌ للغاية، فهو يفسر لنا ظهور نمط التداخل رغم إطلاقنا إلكترونات فردية في تجربة الشقين. مع ذلك، فقد رأينا أنه بقي لدينا عقبة كبيرة، وهي تفسير اختفاء نمط التداخل عند محاولتنا قياس من أي شق عبر الإلكترون بالضبط.
في الواقع، إنّ أبسط تفسيرٍ يمكن أن نضعه لذلك هو أن نضيف قاعدةً جديدةً تنص على أنه قبل قياس الإلكترون، فهو يُمثل بموجةٍ تعبر عن مزيج من جميع النتائج التي يمكن لنا الحصول عليها بعد القياس (في هذه الحالة العبور من الشق الأول أو من الشق الثاني) وهي تعطي نمط تداخل، لكن بمجرد محاولتنا قياس الإلكترون، ستنتج إحدى الحالات الممكنة بعد القياس وليس مزيجاً منها (هنا مثلاً سنجد أنّ الإلكترون قد مرّ من شق محدد) ولذلك يختفي نمط التداخل.
قد تقول لنفسك أنّ هذا مُصطنع للغاية وسخيف، لكن صدق أو لا تصدق، فهذه هي القاعدة المُعتمدة في ميكانيكا الكم للحصول على التنبؤات التجريبية المذهلة لها، والتي هي أساس التكنولوجيا التي نستخدمها في حياتنا اليوم!
ماذا الآن؟
لقد قمنا ببناء نموذجٍ نستطيع استخدامه للحسابات واستخلاص النتائج التجريبية باستخدام القواعد الغريبة المذكورة في الأعلى، وقد نجح هذا النموذج بالفعل نجاحاً مذهلاً للغاية بتفسير المشاهدات التجريبية. إلا أنه يطرح على الصعيد المفاهيمي العديد من المشاكل الكبيرة:
أولاً، ما هي طبيعة هذه الموجة التي تمثل سلوك الإلكترون؟ هل تمثل وجوداً فيزيائياً حقيقياً أم أنها مجرد أداة تساعدنا على القيام بالحسابات؟ وهنا لا بد لي من التنويه لنقطة مهمةٍ لمن يعرف من القراء القليل من الرياضيات، فإذا ما توخيت الدقة، فالاحتمال لا يُحسب من مربع سعة هذه الموجة، بل من مربع القيمة المطلقة لهذه السعة، لأنّ سعة الموجة كما يتبين بالتمحيص ليست مجرد عددٍ موجبٍ أو سالبٍ فقط، بل يمكن أن تكون أيضاً عدداً عقدياً. فما الذي تمثله هذه الموجة بالضبط؟
ثانياً، إنّ الحالة قبل القياس هي مزيج من الحالات الممكنة بعد القياس كما رأينا، وهي مختلفة جذرياً عنها (فقد رأينا أنّ الحالة قبل القياس في تجربة الشق المزدوج قد أعطت نمط تداخلٍ على عكس الحالة بعد القياس، أي حالة عبور الإلكترون من شق مُحدد تماماً). فما هي طبيعة هذه الحالة قبل القياس؟
ثالثاً، ما الذي نعنيه أصلاً بكلمة قياس؟ ومن الذي يقوم بالقياس؟ وما الذي يفعله جهاز القياس بالضبط؟ ولنتخيل معاً الموقف التالي: لنفرض أننا أتينا بجهازٍ لقياس من أي شق مرّ الإلكترون. وهنا يحق لنا أن نسأل السؤال التالي: يمكن أن يكون النظام المكون من جهاز القياس مع الإلكترون حالتين اثنتين: "إلكترون مرّ من الشق الأول وجهاز القياس قد قاسه مرّ من الشق الأول"، أو "إلكترون مرّ من الشق الثاني وجهاز قياس قد قاسه مرّ من الشق الثاني".
إذاً هناك حالتان باحتمالاتٍ محددة، وبالتالي وفق القواعد التي ذكرناها في الأعلى، يجب أن تُمثل بموجة احتمالٍ هي مزيجٌ من الحالتين الممكنتين. بالتالي يجب إجراء قياسٍ لتأخذ حالةً مُحددة من بينهما. حتى في هذه الحالة، فالنظام الجديد المكون من الإلكترون/جهاز قياس، مع جهاز قياس نظام الإلكترون/جهاز قياس، سيحتاج بنفس الطريقة لمن يقيسه ليكون في حالة محددة، وقس على ذلك. فما الذي يحصل بالضبط؟
إن المسائل المطروحة في (ثانياً) و(ثالثاً) تعبّر عما يدعى في ميكانيكا الكم بمشكلة القياس، وهي من أشد مشاكل الفيزياء تأريقاً بالفعل!
هل يعقل أن توصلنا هذه ميكانيكا الكم، التي تُبنى عليها تكنولوجيا هائلة من الليزر إلى الإلكترونيات الحديثة وغيرها، إلى هذه التناقضات والعجائب؟ وهل هناك من تفسير لما يحصل؟
في الواقع، هنالك عدة تفسيرات مطروحة لما يحدث، ولم يُحسم بعد أي منها هو الصحيح، ولكن في كل منها فإنّ ميكانيكا الكم تعطينا صورةً عن العالم أغرب من الخيال. والطريف في الأمر، هو أنّ معظم الناس الذين يستخدمون حواسيبهم وهواتفهم المحمولة كل يوم، لا يدركون أنّ عمل هذه الأجهزة هو إثبات صارخ على صحة نظرية ميكانيكا الكم العجيبة!
سنناقش هنا تفسير كوبنهاغن (21) لميكانيكا الكم، كونه أحد أكثر التفسيرات شيوعاً، وهو التفسير الذي تم وضعه من قبل بعض أهم مؤسسي النظرية الكمومية. ولكن قبل الحديث عنه، فلنلخص ما وصلنا إليه حتى الآن بشكل مقتضب.
تلخيص
في الواقع، إن البنية الرياضية لميكانيكا الكم والناجحة للغاية، تتلخص في النقاط التالية:
1. تُمثل الحالة الفيزيائية بموجة احتمالية (سنقول من الآن فصاعداً دالة موجية) بمعنى أنّ القوانين التي تحكم سلوك الأنظمة الفيزيائية هي قوانين احتمالية وليست قوانين حتمية.
2. تكون الدالة الموجية للأنظمة الفيزيائية قبل القياس عبارةً عن مزيج من الحالات التي يمكن أن نحصل عليها بعد القياس، وهذا ما يُدعى بحالة التراكب، والحالة قبل القياس هي حالة مختلفة جذرياً عن الحالات بعد القياس في الحالة العامة.
3. عند إجراء قياس على النظام، ستظهر فقط إحدى النتائج الممكنة، وهذا ما ندعوه بانهيار الدالة الموجية.
4. ينص مبدأ الارتياب لهايزنبرغ على أنّ هناك بعض المقادير الفيزيائية التي لا يمكن قياسها معاً، لأنه يستحيل تعريفها معاً أصلاً. على سبيل المثال، كما رأينا سابقاً، فإنّ علينا التخلي عن فكرة أنّ الجسيم له مسار كلاسيكي مُحدد تماماً، وهذا يعني بأنه لا يمكن لنا قياس موضعه وسرعته معاً (إذ لو أمكن ذلك في كل نقطة، لكان للجسيم مساراً كلاسيكياً مًحدداً تماماً) وهنا يأتي مبدأ الارتياب، الذي ينص على عدم إمكانية قياس موضع جسيم وسرعته معاً بدقة مطلقة (بشكل أدق يجب أن نستبدل سرعته بزخم حركته التي هي حاصل ضرب كتلته بسرعته). نلاحظ هنا أن مبدأ الارتياب لا علاقة له بدقة الجهاز المُستخدم في القياس أو نوعه، ولا يمكن لنا التملص منه بتحسين أجهزتنا، بل هو من طبيعة قوانين الفيزياء ذاتها.
إن أي تفسير لميكانيكا الكم، هو محاولة لتفسير القواعد السابقة. وسنتناول هنا كما ذكرنا تفسير كوبنهاغن بالذات.
ما الذي يقوله تفسير كوبنهاغن؟
يستند هذا التفسير بشكلٍ كبير على مبدأ التتامية الذي وضعه نيلز بور، والذي ينص على أنّ الأشياء المادية تمتلك صفاتٍ متتامة تأتي في أزواج، ولا يمكن قياسها معاً، بحيث لو امتلك النظام إحدى الصفتين المتتامتين، لما أمكن أن يمتلك الأخرى. بل وإن جهاز القياس هو ما يحدد أي الصفتين المتتامتين ستظهر، ولكل منهما طريقة قياسها الخاصة. إن هذا المبدأ يفسر بشكل رائع مبدأ الارتياب لهايزنبرغ، بالقول أنّ كلاً من الموضع وزخم الحركة هما صفتان متتامتان للجسيم وبالتالي لا يمكن قياسهما معاً. يعني ارتباط الصفة التي ستظهر، بالقياس الذي نقوم به على النظام، أنّ جهاز القياس هو عنصر أساسي كي تظهر هذه الصفة في الطبيعة. بالتالي فما نعرفه من صفات للمادة في الطبيعة هي صفات لها معنى فقط بعد إجراء القياس، أما قبل القياس، فكل ما يمكن الحديث عنه هو احتمالات ما سنحصل عليه بعد القياس، ولا يمكن لنا وضع أي تصور عن الحالة قبل القياس بدلالة المفاهيم التي نعرفها في الفيزياء الكلاسيكية لأنها صفات ليس لها معنى إلا بعد إجراء القياسات التي تعرّفها، وكل ما سبق يعني عدم إمكانية قياس الأنظمة الكمومية دون جعل حالتها تتغير بشكلٍ دراماتيكي!
بهذا المعنى، يعتبر فتفسير كوبنهاغن أنّ الدالة الموجية تزودنا بكل ما نستطيع قوله عن النظام قبل القياس، ولا يوجد متغيرات خفية كلاسيكية يمكن أن نلصقها بالنظام لتصف حالته قبل القياس.
يعتبر تفسير كوبنهاغن أنّ سلوك الأنظمة المكونة من عدد كبير من الجسيمات سيؤول للسلوك الكلاسيكي المألوف على الرغم من أنّ كل جسيمٍ من هذه الجسيمات سيُوصف وفق ميكانيكا الكم.
وعليه، بما أنّ جهاز القياس مكون من عدد كبير من الذرات، فهو سيعطي دوماً نتيجة كلاسيكية مُحددة تماماً (كأن يمرّ الإلكترون من شق محدد تماماً في تجربة الشق المزدوج بعد وضع جهاز القياس) وليس حالةُ غريبة هي عبارة عن مزيجٍ من النتائج الممكنة.
بالتالي وفقاً لهذا التفسير، هناك حدٌّ فاصلٌ بين النظام المدروس، الذي يجب أن يُوصف بدالة موجية، وبين الراصد (الذي يُعد جهاز القياس امتداداً له)، والذي يُوصف كلاسيكياً، وهذا الحد الفاصل يُدعى فاصل هايزنبرغ Heisenberg cut. يعتمد وضع هذا الحد الفاصل على المسألة قيد الدراسة، وهو لذلك اختياريٌ لحد بعيد.
خاتمة
إذاً في الختام، يتبين أنّ تفسير كوبنهاغن يعطي صورةً غايةً في الغرابة عن العالم. إذ تخيل مثلاً أنه لا معنى لمكان الإلكترون قبل أن نقيسه ومع ذلك، فالإلكترون بحد ذاته موجود! ولكن كيف؟ ولماذا؟
في الواقع إنّ تفسير كوبنهاغن هو غريبٌ لدرجة أنّ بعض ألمع الأسماء من مؤسسي ميكانيكا الكم مثل شرودينغر (22) وأينشتاين (23) وغيرهم حاولوا تحديه وبشدة، إلا أنه وفي كل مرة كان أتباع هذا التفسير يستطيعون من خلاله الرد على حجج خصومهم.
على الرغم من أن تفسير كوبنهاغن لم يعد التفسير الوحيد الشائع بين الفيزيائيين، فهو يبقى مثالاً صارخاً على المدى الذي تجبرنا الطبيعة على الخوض فيه من أجل سبر أسرارها.
نُشر هذا المقال بالتعاون مع موقع أراجيك.